Quaternionen sind Elemente einer algebraischen Struktur, die als eine Erweiterung der komplexen Zahlen angesehen werden kann.
Man kann Addition und Multiplikation als innere Operationen der Struktur definieren, so dass die Körperaxiome mit Ausnahme der allgemeinen Kommutativität der Multiplikation gelten.
Man nennt einen solchen Körper auch Schiefkörper.
Quaternionen sind vierdimensionale Objekte, man schreibt sie jedoch zweckmäßigerweise als Skalarkomponente und dreidimensionale Vektorkomponente:
Quaternionenaddition:
Quaternionenmultiplikation:
![\begin{eqnarray*}[a,{\vec v}]\star[b,{\vec w}]&=&[ab-\langle{\vec v},{\vec w}\rangle , \\
& &\;\;a{\vec w}+b{\vec v}+{\vec v}\times{\vec w}]
\end{eqnarray*}](img261.gif)
Man überprüfe als Übung, dass die Körperaxiome erfüllt sind (z.B. Assoziativgesetze und Distributivgesetze).
Quaternionen mit Skalarkomponente gleich Null nennt man auch reine Quaternionen (pure quaternions).
Zusammenfassung der Ähnlichkeiten zwischen komplexen Zahlen und Quaternionen:
| Darstellung | |
|
|
|
| konjugiert | |
| komplex |
|
| gemischtes |
 |
| Produkt |
![$\begin{array}{lcl}
q\bar q &=& [a,{\vec v}]\star[a,-{\vec v}]\\
&=& [a^2-\la...
...{\vec v}]\\
&=& [a^2-\langle{\vec v},-{\vec v}\rangle ,{\vec 0}]
\end{array}$](img267.gif) |
| Betrag |
 |
 |
|
| Kehrwert |
 |
![$\begin{array}{lcl}
1/q &=& \bar q/\vert q\bar q\vert \\
&=& [a,-{\vec v}]/(a^2+\langle{\vec v},{\vec v}\rangle )
\end{array}$](img271.gif) |
Für Einheitsquaternionen, d.h. solche mit Betrag gleich Eins, gilt weiterhin:
Mithilfe der Quaternionen lassen sich Drehungen im Dreidimensionalen sehr einfach spezifizieren und berechnen:
Sei ![]() mit
mit ![]() der normierte Vektor der Rotationsachse
und sei
der normierte Vektor der Rotationsachse
und sei ![]() der gewünschte Rotationswinkel.
der gewünschte Rotationswinkel.
Diese Art und Weise der Spezifikation einer Rotation findet auch in OpenGL Anwendung: glRotateX(...).
Konstruieren Quaternion ![]() wie folgt:
wie folgt:
Interpretieren einen zu rotierenden Punkt mit Ortsvektor ![]() als reinen Quaternion
als reinen Quaternion
Dann ergibt sich der Zielpunkt
![]() wieder in Form eines reinen
Quaternionen als
wieder in Form eines reinen
Quaternionen als
Dieser Abschnitt ist lediglich für den interessierten Leser.
Berechnen wir zuerst einige Beziehungen zwischen Winkel und Halbwinkel, die wir später brauchen werden:
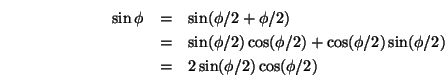
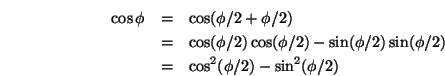
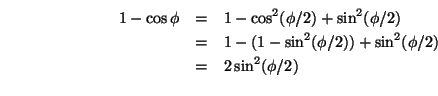
Letztere Gleichung sollte man auch generell zur Berechnung von ![]() benutzen, da sie für kleine
benutzen, da sie für kleine ![]() numerisch wesentlich stabiler
zu berechnen ist.
numerisch wesentlich stabiler
zu berechnen ist.
Führen wir folgende Bezeichnungen und Abkürzungen ein:
zu rotierender Punkt

Rotationsachse
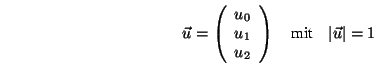
Rotationsquaternion mit Rotationswinkel ![]()
Abkürzungen

Damit schreiben wir also die Rotation nach der Drehformel wie folgt:
Nun berechnen wir eine Matrix ![]() , die die folgende
``Gleichung'' (bei entsprechender Interpretation der
reinen Quaternionen und dreidimensionalen Vektoren) erfüllt:
, die die folgende
``Gleichung'' (bei entsprechender Interpretation der
reinen Quaternionen und dreidimensionalen Vektoren) erfüllt:
![\begin{displaymath}[s,t{\vec u}]\star[0,{\vec x}]\star[s,-t{\vec u}]
=q\star x\...
...=M\cdot\left(\begin{array}{c}x_0\\ x_1\\ x_2\end{array}\right) \end{displaymath}](img289.gif)
und zeigen dann, dass die Matrix ![]() eine Rotationsmatrix
ist, die man sowohl als Produktmatrix aus Achsenrotationsmatrizen
als auch durch direkte Matrizenkonstruktion erhalten kann.
eine Rotationsmatrix
ist, die man sowohl als Produktmatrix aus Achsenrotationsmatrizen
als auch durch direkte Matrizenkonstruktion erhalten kann.
Bemerkung: Wir führen hier keine zusätzliche Translation aus. Diese ist nicht durch Multiplikation mit Quaternionen darstellbar. Man muss also beide Operationen - Rotation und Translation - wieder getrennt betrachten.
Rechnen wir die hamiltonsche Formel aus:
![\begin{eqnarray*}
\lefteqn{[s,t{\vec u}]\star[0,{\vec x}]\star[s,-t{\vec u}]} \\...
...vec u}\times{\vec x})-t^2({\vec u}\times{\vec x})\times{\vec u}]
\end{eqnarray*}](img290.gif)
Wir erkennen als erstes, dass tatsächlich ein reiner Quaternion als Ergebnis entsteht.
Analysieren wir die Vektorkomponente.
Hierzu notieren wir zuerst die Vektorprodukte mit Koordinatenwerten:
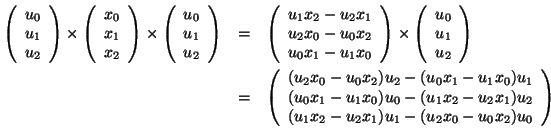
Formulieren wir damit die ![]() -Komponente des Resultatsvektors
aus:
-Komponente des Resultatsvektors
aus:

Nun kann man unter Zuhilfenahme von
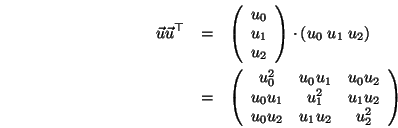
und analogem Formulieren der anderen Komponenten (Übung) das Ergebnis in folgender Art notieren:

Und wir erhalten durch Ersetzen der Abkürzungen und Anwenden der Halbwinkelbeziehungen von oben folgende Darstellung:

Was hat dies mit der Rotationsmatrix zu tun?
Betrachten wir nochmals die ![]() -Achsenrotationsmatrix
und schreiben diese auch als eine geschickte Summe
von Matrizen, wobei wir erst wieder ein paar Kurznotationen
einführen:
-Achsenrotationsmatrix
und schreiben diese auch als eine geschickte Summe
von Matrizen, wobei wir erst wieder ein paar Kurznotationen
einführen:

Damit erhalten wir:
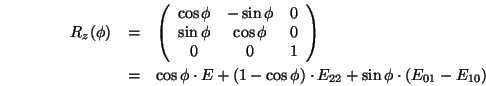
Multiplizieren wir nun diese ![]() -Rotationsmatrix von
links und rechts mit einer orthonormalen Matrix
-Rotationsmatrix von
links und rechts mit einer orthonormalen Matrix ![]() ,
die wir mit
,
die wir mit ![]() und zwei dazu senkrechten Vektoren
und zwei dazu senkrechten Vektoren ![]() und
und
![]() , d.h.
, d.h.
![]() als
als
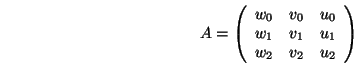
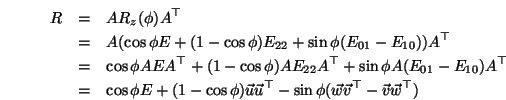
und letztlich

was genau dem obigen Ausdruck entspricht.