Generell kann jede Drehung mit einem Winkel ![]() um eine
beliebige Achse auch durch Hintereinanderausführen von bis
zu drei Drehungen um Koordinatenachsen ausgeführt werden, wobei
zwei aufeinander folgende Drehungen nicht um die gleiche Achse
durchgeführt werden dürfen (Eulers Theorem).
um eine
beliebige Achse auch durch Hintereinanderausführen von bis
zu drei Drehungen um Koordinatenachsen ausgeführt werden, wobei
zwei aufeinander folgende Drehungen nicht um die gleiche Achse
durchgeführt werden dürfen (Eulers Theorem).
Da die Ausführung von Rotationen nicht kommutativ ist, ergeben sich 12 mögliche Kombinationen:
Verwendet man Eulerwinkel sollte man stets auf die zugrundeliegende
Reihenfolge achten!
Gebräuchliche Kombinationen sind: ![]() und
und ![]() .
.
Betrachten wir die ![]() -Kombination mit den Winkeln
-Kombination mit den Winkeln
![]() ,
, ![]() und
und ![]() .
.
Die Rotationsmatrix (in kartesischen Koordinaten) berechnet sich dann:
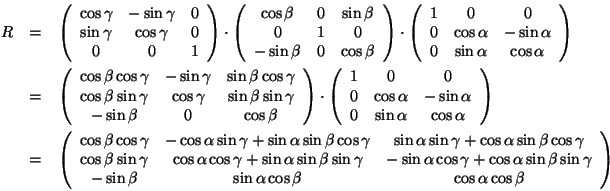
Stellt sich für ![]() ein Winkel von
ein Winkel von ![]() (oder
(oder ![]() ) ein,
d.h.
) ein,
d.h. ![]() und
und ![]() so ergibt sich:
so ergibt sich:
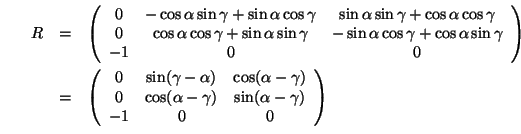
und wir erkennen, dass ein Freiheitsgrad eingebüßt wurde,
jede Änderung von ![]() oder
oder ![]() ergibt eine Drehung um
die selbe Drehachse.
ergibt eine Drehung um
die selbe Drehachse.
Dieses Phenomen wird als Gimbal-Lock bezeichnet und bereitet insbesondere bei dreiachsigen mechanischen Navigierungsgeräten als auch bei Benutzerschnittstellen Probleme.