Rotation

Trigonometrische Additionstheoreme

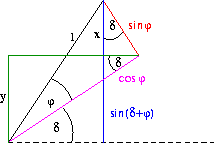
Wie bei vielen trigonometrischen Beweisen liegt der Trick im Einzeichnen der richtigen Hilfslinien und Anwenden einfacher Beziehungen.

$$\begin{eqnarray*} \frac{x}{\sin\varphi} &=& \cos\delta \\ \frac{y}{\cos\varph... ...&=& x+y \\ &=& \cos\delta\,\sin\varphi+\sin\delta\,\cos\varphi \end{eqnarray*}$$

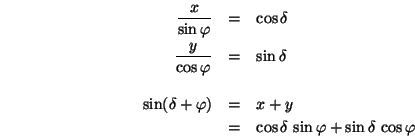
Man überprüft leicht, dass die Formel auch für $\varphi=0$ gilt.

Entsprechend kann man auch das Additionstheorem für den $\cos$ herleiten (tun Sie dies) und erhält:

$$\cos(\delta+\varphi) = \cos\delta\,\cos\varphi-\sin\delta\,\sin\varphi$$

Rotation um eine Koordinatenachse

zweidimensionale Fall:

Durch Anwendung der Additionstheoreme können wir eine Rotation eines Punktes um den Koordinatenursprung berechnen:

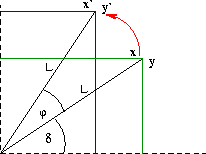
Wir sehen in der Abbildung:

$$\begin{eqnarray*} \sin(\delta+\varphi) &=& y^\prime/L \\ &=& \cos\delta\,\sin\... ...cdot \cos\varphi \cdot y/L \\ &=& x\sin\varphi + y\cos\varphi \end{eqnarray*}$$

und entsprechend

$$\begin{eqnarray*} \cos(\delta+\varphi) &=& x^\prime/L \\ &=& \cos\delta\,\cos\... ...cdot \sin\varphi \cdot y/L \\ &=& x\cos\varphi - y\sin\varphi \end{eqnarray*}$$

und dies in Matrizenschreibweise:

• in kartesischen Koordinaten
  
  $$\left(\begin{array}{c}x^\prime\\ y^\prime\end{array}\right)... ...ray}\right)\cdot\left(\begin{array}{c}x\\ y\end{array}\right)$$
  
  

• in homogenen Koordinaten
  
  $$\left(\begin{array}{c}x_0^\prime\\ x_1^\prime\\ x_2^\prime\... ... \cdot\left(\begin{array}{c}x_0\\ x_1\\ x_2\end{array}\right)$$
  
  

Die Umkehrung erhält man durch eine Drehung um den Winkel $-\varphi$, also

• in kartesischen Koordinaten
  
  $$\left(\begin{array}{c}x\\ y\end{array}\right) = \left(\beg... ...ot\left(\begin{array}{c}x^\prime\\ y^\prime\end{array}\right)$$
  
  

• in homogenen Koordinaten
  
  $$\left(\begin{array}{c}x_0\\ x_1\\ x_2\end{array}\right) = ... ...ray}{c}x^\prime_0\\ x^\prime_1\\ x^\prime_2\end{array}\right)$$
  
  

dreidimensionale Fall:

Aus dem zweidimensionalen Fall erhalten wir direkt die Rotationen um Koordinatenachsen im Dreidimensionalen, z.B. eine Rotation um die $z$-Achse:

• in kartesischen Koordinaten
  
  $$\left(\begin{array}{c}x^\prime_0\\ x^\prime_1\\ x^\prime_2\... ...{c}x_0\\ x_1\\ x_2\end{array}\right) = R_z(\varphi)\,{\vec x}$$
  
  

• in homogenen Koordinaten
  
  $$\left(\begin{array}{c}x^\prime_0\\ x^\prime_1\\ x^\prime_2\... ...ot\left(\begin{array}{c}x_0\\ x_1\\ x_2\\ 1\end{array}\right)$$
  
  

Rotationen um die anderen Koordinatenachsen erhält man durch zyklisches Vertauschen der Koordinaten, d.h. $x\longrightarrow y\longrightarrow z\longrightarrow x$.

Rotation um einen beliebigen Punkt oder Achse

Tafelerklärung