Man möchte lineare Abbildungen ![]() betrachten, d.h. Geraden vor
der Abbildung bleiben Geraden nach der Abbildung, also muss die
Abbildung
betrachten, d.h. Geraden vor
der Abbildung bleiben Geraden nach der Abbildung, also muss die
Abbildung ![]() speziell mit der Skalarmultiplikation und der Vektoraddition
verträglich sein:
speziell mit der Skalarmultiplikation und der Vektoraddition
verträglich sein:
in Worten heißt dies: es soll egal sein, ob man die Vektoren vor oder nach Anwendung der Abbildung streckt/kürzt oder addiert.
Multipliziert man einen Vektor von links mit einer Matrix, so stellt dies eine affine Vektorabbildung dar:
Dies sieht man leicht durch Anwenden der entsprechenden Rechenregeln für Vektoren und Matrizen ein:
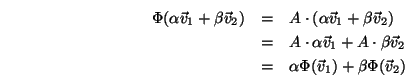
Ist die Matrix ![]() singulär, dann bezeichnet man die
affine Abbildung als entartet (hierzu zählen die Projektionen).
singulär, dann bezeichnet man die
affine Abbildung als entartet (hierzu zählen die Projektionen).
Im Folgenden betrachten wir--sofern nicht speziell vermerkt--nur nicht-entartete affine Abbildungen.
Der Verschiebungsvektor ist bereits eindeutig festgelegt, wenn man
sich die Matrix ![]() und einen Punkt mit seinem Bildpunkt vorgibt.
und einen Punkt mit seinem Bildpunkt vorgibt.
Insbesondere kann man eine affinepointaffine Punktabbildung konstruieren, wenn man sich lediglich vier nicht in einer Ebene liegende Punkte und deren gewünschten Bildpunkte vorgibt:
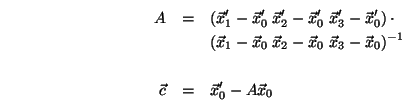
Eigenschaften der affinen Abbildungen: