Affine Kombination

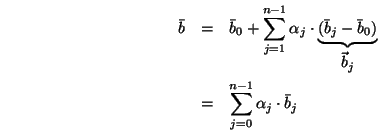
oder auch barizentrische Kombination

Eine affine Kombination ist eine gewichtete Summe von Punkten; dies ist jedoch keine eigentliche Summe von Punkten (was nicht definiert wäre) sondern eine Summe von Differenzen von Punkten, also letztlich eine gewichtete Summe von Vektoren zu einem Punkt.

$$\begin{eqnarray*} \bar b &=& \bar b_0 + \sum_{j=1}^{n-1}\alpha_j\cdot \underbr... ...ystyle{\vec b}_j} \\ &=& \sum_{j=0}^{n-1}\alpha_j\cdot\bar b_j \end{eqnarray*}$$

wobei für die Gewichte $\alpha_j$ gilt:

$$\begin{eqnarray*} \sum_{j=0}^{n-1}\alpha_j&=&1 \end{eqnarray*}$$

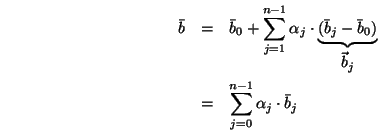
Wählt man alle Gewichte gleich $1/n$, so erhält man eine Art Schwerpunkt:

$$\begin{eqnarray*} \bar b&=&\frac{1}{n}\sum_{j=0}^{n-1}\bar b_j \end{eqnarray*}$$

Sind alle Gewichte größer Null, dann spricht man von konvexer Kombination, der konstruierte Punkt liegt dann in der konvexen Hülle der Punkte.