Geometrie von Lichtquellen

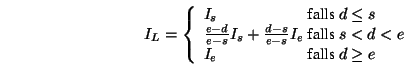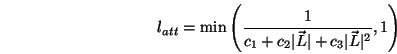
Unter den geometrischen Eigenschaften von Lichtquellen ist weniger der tatsächliche Aufbau der Lichtquelle gemeint, sondern vielmehr die Verteilung der Intensität in den umgebenden Raum. Dies löst oft in empirischer Hinsicht das Problem, die Intensitätsabschwächung bzgl. des Abstandes der strahlungserzeugenden von der strahlungsempfangenden Fläche bzw. einfache Eigenschaften einer Atmosphere in die Modellierung gut einzubeziehen.

Empirische Licht-Abschwächung

Foley und van Dam (1991) schlagen desweiteren den folgenden Abschwächungsfaktor vor:

$$l_{att} = \min\left(\frac{1}{c_1+c_2\vert\vec{L}\vert+c_3\vert\vec{L}\vert^2},1\right)$$

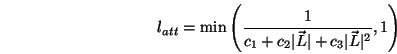
wobei die Konstanten Parameter der Lichtquelle sind.

Warn-Lichtquellen

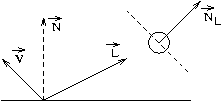
Warn (1983) modelliert eine Lichtquelle mithilfe des Phongschen Kosinus-Terms. Hierbei wird zusätzlich zum Ort der Lichtquelle ein Normalenvektor $\vec{N}_L$ definiert. Die Intensität ergibt sich dann:

$$I_L = I_{max}\;\langle \vec{L},\vec{N}_L\rangle ^p$$

dabei ist $p$ wiederum ein Parameter, der den Durchmesser des spot lights festlegt.

Es besteht auch die Möglichkeit die Intensität des Lichtes mithilfe eines binären Faktors $b_L$ auf bestimmte Regionen des Raumes einzuschränken. Als Beispiele werden von Warn folgende Regionen genannt: Kegel, Spalten (Räume zwischen zwei Ebenen), Würfel um die Punktlichtquelle.

Entfernungsabschächung

Um beispielsweise die Intensität einer Lichtquelle einfach mit der Entfernung zu variieren (Fading oder depth cueing), kann man folgende Gleichung verwenden:

$$I_L = \left\{\begin{array}{l@{\mbox{~falls~}}l} I_s & d\leq... ...c{d-s}{e-s}I_e & s<d<e \\ I_e & d \geq e \end{array}\right.$$

Dabei sind $s$ und $e$ Start- bzw. Endwert einer linearen Fade-Funktion. $d$ ist der Abstand zur Lichtquelle $\vert\vec{L}\vert$ oder der Abstand zum Betrachter $\vert\vec{V}\vert$ je nach gewählter Modellierung. Dies kann in einen Abschwächungsfaktor integriert werden.