Zur besseren Gliederung und einfacheren Referenzierung werden im folgenden die Modelle in der Reihenfolge ihres Auftretens nummeriert. Die Modelle sollten nicht nur für einen speziellen Darstellungsalgorithmus angesehen werden, sondern sie können je nach erforderlichen Parameter für die verschiedenen Verfahren genutzt werden.
Generell sei bemerkt, dass eine Lichtquelle in Richtung ![]() nur
dann einen Beitrag zur Intensität an einer Oberfläche mit Normalenvektor
nur
dann einen Beitrag zur Intensität an einer Oberfläche mit Normalenvektor
![]() leistet, wenn gilt:
leistet, wenn gilt:
Das ambiente Modell bleibt mithilfe des Superpositionsprinzip in den Darstellungsmodellen erhalten, d.h. dort wird ein Teil der Intensität aufgrund obiger Vorschrift berechnet. Dies garantiert eine Grundhelligkeit in der darzustellenden Szene, da gerade viele Verfahren die indirekte, diffuse Beleuchtung von Oberflächen durch Reflexionen von anderen Objekten ungenügend modellieren. Eine Ausnahme bildet das Radiosity-Verfahren, das speziell diesen Aspekt der Beleuchtung berücksichtigt.
Vorgreifend auf die abschließende
Zusammenfassung sei hier schon gesagt, dass alle Beleuchtungsmodelle
(mit Ausnahme von Radiosity) die Intensität an einem Punkt
gemäß folgender Vorgehensweise berechnen:
Cook und Torrence führten einen durch die Geometrie der Szene
bestimmten Abschwächungsfaktor ![]() ein, der den ambienten
Intensitätsanteil beeinflussen soll. (
ein, der den ambienten
Intensitätsanteil beeinflussen soll. (![]() ist ein Objektparameter
und
ist ein Objektparameter
und ![]() ein der gesamten Szenen gegebener Parameter.)
ein der gesamten Szenen gegebener Parameter.)
Allerdings wird dessen Berechnung nicht weiter ausgeführt. Man könnte ihn als eine frühe Vorwegnahme des Radiosity-Ansatzes interpretieren.
Hier wird die Position des Betrachters nicht berücksichtigt, d.h. die darzustellende Intensität ist nicht vom Betrachterwinkel ![]() abhängig.
abhängig.
was bei punktförmigen Lichtquellen zu
Sind ![]() Lichtquellen vorhanden, erhält man durch Superposition:
Lichtquellen vorhanden, erhält man durch Superposition:
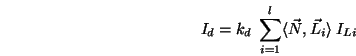
Dieses Superpositionsprinzip kann sinngemäß auf alle folgenden Modelle angewandt werden und wird vereinfachend nicht stets explizit angegeben.
Bis jetzt wurde die Betrachterposition sowie die Entfernung zur Lichtquelle noch nicht berücksichtigt.
An dieser Stelle seien zwei frühe, einfache, empirisch begründete Modelle angeführt, die zur Darstellung von ``Grau-Szenen'' verwendet worden sind, mehr wohl mit dem Hintergrund, Ergebnisse von Darstellungsalgorithmen zu dokumentieren. Insbesondere ist die Intensität einer Oberfläche nicht von der Entfernung der Oberfläche von der Lichtquelle, sondern von der Entfernung vom Betrachter abhängig.


Hier wurden die Flächen auch von hinten gezeichnet; es gab anscheinend noch keine komplexeren Objekte, wie sie heute verwendet werden. Hier kann das Skalarprodukt auch negativ sein.
Die Lichtquellen wurden bisher als Punktlichtquellen modelliert, was
keine Berechnung von Raumwinkeln, aus denen ein Objekt beleuchtet
wird, erlaubt. Insbesondere sinkt die Intensität mit wachsender
Entfernung von der Lichtquelle mit ![]() , wie wir oben gesehen
haben.
, wie wir oben gesehen
haben.
Dabei ist ![]() der Raumwinkel, unter dem die Lichtquelle von
der Fläche aus gesehen wird.
der Raumwinkel, unter dem die Lichtquelle von
der Fläche aus gesehen wird.
Mögliche Interpretation: Modelliert man die Lichtquellen als
Kugeln und sind sie weit von der bestrahlten Fläche
entfernt (Abstand ![]() ), kann man die Näherung
), kann man die Näherung

Nun kann man auch das Abschwächen der Strahlung auf dem Weg der
Länge ![]() vom Objekt zum Betrachter berücksichtigen:
vom Objekt zum Betrachter berücksichtigen:

Mögliche Interpretation: Eigentlich müsste die Entfernung zum Betrachter wie folgt in das Modell eingebaut werden:

Da die reflektierte Intensität--sozusagen, ab dem Punkt ihrer Erzeugung--quadratisch mit dem Abstand vom Betrachter abnimmt. Dieses belegt auch möglicherweise die frühen, guten Ergebnisse von Romney (Modell 5).
Modell 6 hat den Nachteil, dass der Raumwinkel ![]() der
Lichtquelle bekannt sein muss. Verwendet man die Näherung (Modell 7)
oder auch die Modelle 8 und 9, die jeweils den Abstand berücksichtigen,
ergeben sich zwei Probleme: bei unendlich weit entfernten Lichtquellen
kann die Gleichung nicht verwendet werden, bei geringem Abstand zwischen
Lichtquelle und Objekt ist die Näherung nicht gültig und man erzielt
schlechte Resultate. Deshalb wurden weiter folgende Lösungen
vorgeschlagen:
der
Lichtquelle bekannt sein muss. Verwendet man die Näherung (Modell 7)
oder auch die Modelle 8 und 9, die jeweils den Abstand berücksichtigen,
ergeben sich zwei Probleme: bei unendlich weit entfernten Lichtquellen
kann die Gleichung nicht verwendet werden, bei geringem Abstand zwischen
Lichtquelle und Objekt ist die Näherung nicht gültig und man erzielt
schlechte Resultate. Deshalb wurden weiter folgende Lösungen
vorgeschlagen:

Die Modelle 7 bis 10 kann man wie folgt zusammenfassen:
wobei ![]() ein sogenannter Abschwächungsfaktor
(attenuation factor)
ist; hier bezüglich der Entfernung. Mit Hilfe von Abschwächungsfaktoren
können auch andere Effekte, wie Atmospheren, modelliert werden.
Weitere Möglichkeiten der Beeinflussung der Eigenschaften der
Lichtquelle werden in späteren Abschnitten erläutert.
ein sogenannter Abschwächungsfaktor
(attenuation factor)
ist; hier bezüglich der Entfernung. Mit Hilfe von Abschwächungsfaktoren
können auch andere Effekte, wie Atmospheren, modelliert werden.
Weitere Möglichkeiten der Beeinflussung der Eigenschaften der
Lichtquelle werden in späteren Abschnitten erläutert.
(Hier würde es mit Radiosity weitergehen.)
Eines der ersten, frühen Modelle ist:

Lichtquelle und Betrachter müssen im gleichen Punkt liegen. Eine Verbesserung wurde von Phong vorgeschlagen:
Die Größe der Materialkonstanten ![]() bestimmt die Größe eines
Schlaglichtes (highlights) auf der bestrahlten Fläche.
Ursprünglich war
bestimmt die Größe eines
Schlaglichtes (highlights) auf der bestrahlten Fläche.
Ursprünglich war
![]() ein vom Einfallswinkel
ein vom Einfallswinkel ![]() abhängiger Materialparameter, der
empirisch bestimmt wurde. Foley und van Dam benutzen allerdings später nur
eine Konstante und erhalten trotzdem ``zufriedenstellende'' Bilder, allerdings
wird wiederum die Entfernung vom Betrachter eingebracht:
abhängiger Materialparameter, der
empirisch bestimmt wurde. Foley und van Dam benutzen allerdings später nur
eine Konstante und erhalten trotzdem ``zufriedenstellende'' Bilder, allerdings
wird wiederum die Entfernung vom Betrachter eingebracht:

Um nun nicht den Reflexionsvektor ![]() berechnen zu müssen, kann
man ihn durch den Halbvektor
berechnen zu müssen, kann
man ihn durch den Halbvektor ![]() und den Betrachtervektor
und den Betrachtervektor ![]() durch den Normalenvektor
durch den Normalenvektor ![]() ersetzen. Es gilt also:
ersetzen. Es gilt also:
Analog kann man wiederum den Abstand integrieren:

Yang führte ein modifiziertes Modell nach Phong ein, bei dem der highlight-Faktor geringfügig anders berechnet wird:
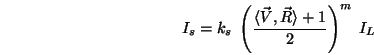
Die oben gemachte Modellierung der Oberflächeneigenschaften kann wie folgt in die Berechnung der Intensität integriert werden:
Dabei benutzt Blinn
![]() und für
und für ![]() die
Verteilungen
die
Verteilungen ![]() ,
, ![]() und
und ![]() . Hierbei stellt er fest,
dass die Verteilungen sich sehr ähnlich sind. Fordert man, dass
. Hierbei stellt er fest,
dass die Verteilungen sich sehr ähnlich sind. Fordert man, dass
![]() für alle drei Verteilungen an der gleichen
Stelle
für alle drei Verteilungen an der gleichen
Stelle
![]() ist, kann man die
Materialkonstanten
ist, kann man die
Materialkonstanten ![]() ,
, ![]() und
und ![]() auf einen einzigen Winkel
auf einen einzigen Winkel
![]() als Materialkonstante zurückführen:
als Materialkonstante zurückführen:
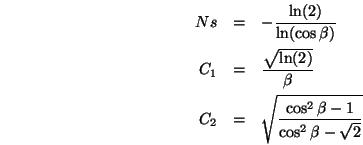
Auch hier kann die Konstante ![]() in
in ![]() wieder auf den Winkel
wieder auf den Winkel ![]() zurückgeführt werden:
zurückgeführt werden:
Test lassen jedoch die Formel
Dieses Modell geht davon aus, dass die Oberflächen relativ rauh gegenüber der Wellenlänge des Lichtes sind, da nur die letzte Gleichung der Beckmannschen Gleichungen verwendet worden ist. Insbesondere heißt dies, dass man die Verteilung nicht für sehr glatte, spiegelnde Oberflächen einsetzen sollte.
Für die geometrische Abschwächung kann auch die Funktion ![]() nach
Sancer in den Modellen 18 und 19 eingesetzt werden.
nach
Sancer in den Modellen 18 und 19 eingesetzt werden.
Torrance und Greenberg führten 1991 ein neues, physikalisch begründetes
Modell ein, das auch in der Lage ist, Polarisationseffekte zu beschreiben.
Auf die Polarisationseffekte wird hier nicht eingegangen, sondern lediglich
das vereinfachte Modell wiedergegeben, welches die Abschwächungsfaktoren,
wie sie weiter oben erläutert worden sind, verwendet.
Ein wesentlicher Punkt in diesem
Modell ist die Tatsache, dass der spiegelnde Intensitätsanteil
erneut in zwei Anteile aufgespalten worden ist.
Für den diffusen Lichtanteil ![]() wird weiterhin das Modell 6 benutzt.
wird weiterhin das Modell 6 benutzt.
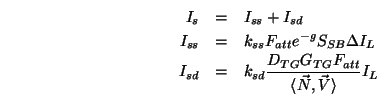
![]() ist die Selbstbeschattungsfunktion nach Smith und Bruce.
ist die Selbstbeschattungsfunktion nach Smith und Bruce.
![]() ist eine Delta-Funktion, die entscheided, ob der betrachtete
Strahl im sogenannten Spiegelkegel liegt, d.h. einem kleinen Raumwinkel,
indem man spiegelnde Reflexion erwartet. Man kann
ist eine Delta-Funktion, die entscheided, ob der betrachtete
Strahl im sogenannten Spiegelkegel liegt, d.h. einem kleinen Raumwinkel,
indem man spiegelnde Reflexion erwartet. Man kann ![]() z.B. wie
folgt berechnen:
z.B. wie
folgt berechnen:
Das einfachste Modell berücksichtigt keine Brechungseffekte und macht die Annahme von unendlich dünnen Oberflächen:
Dabei ist ![]() die Intensität, die durch das im Hintergrund liegende
Objekt erzeugt wird.
die Intensität, die durch das im Hintergrund liegende
Objekt erzeugt wird. ![]() ist der Teil der Intensität, der ohne
Transparenz berechnet würde. Man erkennt, das dieses Modell einfach
eine lineare Interpolation der beiden Intensitäten ist.
ist der Teil der Intensität, der ohne
Transparenz berechnet würde. Man erkennt, das dieses Modell einfach
eine lineare Interpolation der beiden Intensitäten ist. ![]() gibt
die Transmissionsrate an.
gibt
die Transmissionsrate an.
In einfachen Darstellungsalgorithmen kann man die Transparenzrate von der Dicke des Objektes in Blickrichtung (vorallem bei parallel Projektionen) abhängig machen. Dies wurde von Crow wie folgt vorgeschlagen:
Die Berechnung der Intensität bleibt analog zu Modell 20.
Hierbei ist vereinfachend davon ausgegangen, dass der Betrachter in
![]() -Richtung blickt.
-Richtung blickt.
Die Modellierung von Transparenz ist wesentlich schwieriger als die von Reflexion und wurde auch nicht so stark verfolgt wie diese. Das folgende Modell beinhaltet viele Vereinfachungen, kann jedoch für einzelne Strahlverfolgungen nach dem Snellschen Gesetz eingesetzt werden.

Der Brechungsindex ist von der Wellenlänge abhängig, was man für
Dispersion ausnutzen kann. Bei transparenten Materialien muss man
berücksichtigen, dass beim Verlauf der Strahlung durch das Material
eine Abschwächung ![]() --analog zu einem atmospherischen
Effekt--auftritt,
die ebenfalls von der Wellenlänge abhängig sein kann. So ist
zum Beispiel in Wasser die Absorptionsrate von grünem Licht am
geringsten.
--analog zu einem atmospherischen
Effekt--auftritt,
die ebenfalls von der Wellenlänge abhängig sein kann. So ist
zum Beispiel in Wasser die Absorptionsrate von grünem Licht am
geringsten.
Durch Superposition und je nach verwendetem Darstellungsalgorithmus können also die folgenden Lichtanteile, die je nach gewünschtem Modell berechnet werden, überlagert werden:
| ambienter Lichtanteil | |
| diffuser Lichtanteil | |
| durch Reflexion erzeugter Lichtanteil | |
| (in Modell 20 wiederum aufgespalten) | |
| durch Transparenz erzeugter Lichtanteil |
In den Modellen wurden folgende Abschwächungsfaktoren eingeführt, die je nach Modell unterschiedliche Materialparameter notwendig machen:
| Fresnel-Abschwächung | |
| Verteilungsabschwächung | |
| geometrische Abschwächung | |
| Abschwächung durch Selbstbeschattung | |
| Entfernungsabschwächung | |
| Absorptionsabschwächung |