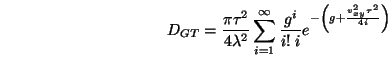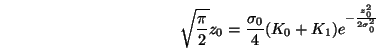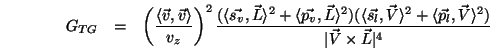Nächste Seite: Berechnungsmodelle
Aufwärts: Beleuchtungsmodelle hin zur fotorealistischen
Vorherige Seite: Strahlungslehre
Inhalt
Unterabschnitte
Die Theorie, die ansatzweise oben besprochen worden ist, beschreibt
nur ideale Oberflächen. Reale Oberflächen sind jedoch auch durch folgende
Eigenschaften gekennzeichnet:
- Sie bestehen aus keinem einheitlichen Material, dessen optischen
Eigenschaften bekannt (?) sind.
- Sie sind nicht optisch glatt, d.h. die optischen Eigenschaften werden
auch durch Mikro-Geometrie bestimmt.
- Es sind keine exakten Modelle zur Beschreibung der Materialien und der
Oberflächen bekannt.
- Man kennt nicht genügend Messdaten, um die obigen Formeln sinnvoll
anwenden zu können.
- Die einfallende Strahlung wechselwirkt mit dem gesamten Material, d.h. sie dringt in das Material ein und unterliegt dort wiederum anderen
physikalischen Gesetzen. (Diese Effekte sind insbesondere bei dünnen
Farbfilmen auf Metallen zu beachten.)
Metalle haben eine relativ geringe Emmisionsrate 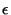 und damit
auch eine geringe Absorptionsrate
und damit
auch eine geringe Absorptionsrate  . Demzufolge ist die Reflexionsrate
. Demzufolge ist die Reflexionsrate
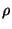 relativ hoch. Es gelten die folgenden Beziehungen:
relativ hoch. Es gelten die folgenden Beziehungen:
- Mit steigendem Einfallswinkel
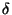 steigt die
Emmisionsrate
steigt die
Emmisionsrate 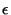 und damit sinkt die Reflexionsrate
und damit sinkt die Reflexionsrate 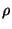 , d.h. je flacher man auf eine Metallplatte schaut, umso weniger spiegelt sie.
, d.h. je flacher man auf eine Metallplatte schaut, umso weniger spiegelt sie.
- Mit steigender Wellenlänge
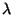 sinkt die Emmisionsrate
sinkt die Emmisionsrate 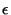 und damit steigt die Reflexionsrate
und damit steigt die Reflexionsrate 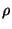 . Kupfer macht hierbei eine
Ausnahme:
. Kupfer macht hierbei eine
Ausnahme: 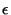 ist relativ konstant bezüglich
ist relativ konstant bezüglich 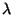 .
.
- Mit steigender Temperatur
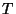 steigt die Emmisionsrate
steigt die Emmisionsrate 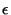 und damit sinkt die Reflexionsrate
und damit sinkt die Reflexionsrate 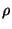 .
.
- Für gewisse Wellenlängen- und Temperaturbereiche ist die
Emmisionsrate proportional zum elektrischen Widerstand des Metalles.
Optische Materialeigenschaften von Nicht-Metallen sind noch
weniger bekannt als die der Metalle. Nicht-Metalle verhalten sich
oft umgekehrt wie Metalle, insbesondere sinkt die Emmisionsrate
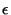 mit steigendem Einfallswinkel
mit steigendem Einfallswinkel 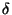 , d.h. schaut
man flach auf eine Nicht-Metallplatte, spiegelt sie mehr als bei direkter
Draufsicht.
Die Wellenlängenabhängigkeiten sind deutlich geringer als die der
Metalle. Dies gilt ebenso für die Temperaturabhängigkeit.
Mit anderen Worten, der
Brechungsindex ist annähernd konstant bezüglich
, d.h. schaut
man flach auf eine Nicht-Metallplatte, spiegelt sie mehr als bei direkter
Draufsicht.
Die Wellenlängenabhängigkeiten sind deutlich geringer als die der
Metalle. Dies gilt ebenso für die Temperaturabhängigkeit.
Mit anderen Worten, der
Brechungsindex ist annähernd konstant bezüglich 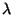 und
und 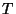 .
.
Eine Oberfläche kann--sofern sie keine Verwerfungen aufweist--als
eine zweidimensionale Funktion 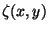 aufgefasst werden.
Für einen Punkt
aufgefasst werden.
Für einen Punkt 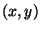 gibt
gibt 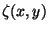 die Abweichung der
Oberfläche vom Mittelwert an. Es gilt somit:
die Abweichung der
Oberfläche vom Mittelwert an. Es gilt somit:
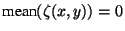 .
Für die Standardabweichung
.
Für die Standardabweichung 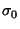 gilt:
gilt:
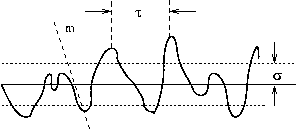
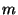 |
mittlere Steigung |
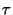 |
mittlere Berg/Talabstand (correlation distance) |
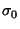 |
mittlere Abweichung vom Mittelwert |
Für die Beziehungen zwischen den drei Parametern wird von Beckmann
(1963) aufgrund einer einfachen geometrischen Anschauung
und von Bennett (1961)
angegeben. Die zweite Formel ergibt sich unter der Annahme, dass
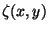 Gauss-verteilt ist. Ein korrekter Wert ergibt sich
nur aus der tatsächlichen Verteilung.
Gauss-verteilt ist. Ein korrekter Wert ergibt sich
nur aus der tatsächlichen Verteilung.
Nun kann man zwei Phenomene unterscheiden. Zum einen werden die
Reflexionseigenschaften des Materials geändert, da die Oberfläche
nicht mehr wie im theoretischen gefordert orientiert ist, was eine
Reduktion der Reflexionsrate zur Folge hat. Dies wird durch zwei
Reduktionsfaktoren 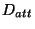 und
und 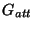 zum Ausdruck gebracht.
Zum anderen wird
möglicherweise reflektiertes oder einfallendes Licht durch die
Oberfläche selbst
abgeblockt--man könnte Selbstbeschattung sagen, was ebenfalls
die Reflexionsrate reduziert. Dies kann durch einen
Abschwächungsfaktor
zum Ausdruck gebracht.
Zum anderen wird
möglicherweise reflektiertes oder einfallendes Licht durch die
Oberfläche selbst
abgeblockt--man könnte Selbstbeschattung sagen, was ebenfalls
die Reflexionsrate reduziert. Dies kann durch einen
Abschwächungsfaktor 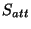 modelliert werden.
modelliert werden.
Bemerkung: In der Literatur wird 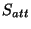 oft mit
oft mit 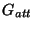 bezeichnet, sowie
bezeichnet, sowie
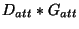 als
als 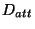 zusammengefasst.
zusammengefasst.
Wir wollen drei Abschwächungsfaktoren angeben.
- Torrance und Sparrow (1963) führten eine geometrische Selbstabschwächung
nach einem einfachen Oberflächenmodell ein.
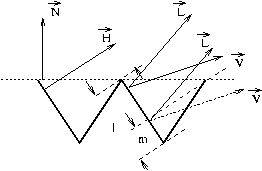
Es ergibt sich:
Dieser Faktor hat die Nachteile, dass er nicht stetig und nicht symmetrisch
ist,
- was bei dem
Faktor nach Sancer (1969), der mithilfe von Normalverteilungen
hergeleitet ist, nicht der Fall ist.
Dabei sind die Werte für 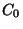 und
und  relativ kompliziert
zu berechnen:
relativ kompliziert
zu berechnen:
d.h. 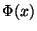 berechnet das Gausssche Fehlerintegral. Dies ist
in mathematischen Bibliotheken (C-Compiler) als erf() enthalten.
Auch die Funktion
berechnet das Gausssche Fehlerintegral. Dies ist
in mathematischen Bibliotheken (C-Compiler) als erf() enthalten.
Auch die Funktion 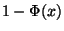 ist als erfc() vorhanden. Für
den Sancer-Faktor ist eine weitere Materialeigenschaft
ist als erfc() vorhanden. Für
den Sancer-Faktor ist eine weitere Materialeigenschaft
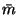 notwendig,
was bei Torrance und Sparrow nicht erforderlich ist.
notwendig,
was bei Torrance und Sparrow nicht erforderlich ist.
- Torrance und Greenberg verwenden einen Faktor nach Smith und Bruce,
der noch komplizierter zu berechnen ist:
(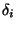 und
und  wie oben.)
Hier kann auch wiederum
wie oben.)
Hier kann auch wiederum 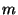 eingesetzt werden.
eingesetzt werden.
Die Oberfläche wird nicht mehr als einheitliche Fläche, sondern als
Ansammlung von Micro-Facetten beschrieben, von denen nur diejenigen
zu einer Reflexion beitragen, die entsprechend orientiert sind. Es
kommt also auf die Verteilung und die geometrische Anordnung
der Micro-Facetten innerhalb der
Oberfläche an. Dies kann durch zwei Faktoren 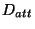 und
und 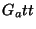 modelliert werden. Als mögliche Verteilungen wurden die folgenden
vorgeschlagen:
modelliert werden. Als mögliche Verteilungen wurden die folgenden
vorgeschlagen:
- Phong
-
Diese Verteilung wird in den meisten einfachen Modellen (siehe Beschreibung
der Modelle) verwendet. Sie ist für das Entstehen von Schlaglichtern
verantwortlich.
- Torrance and Sparrow (1967)
- Auch diese Verteilung ist recht einfach, wurde jedoch selten
benutzt.
- Trowbridge und Reitz (1967)
- Eine weitere Verteilung ist
- Beckmann und Bahar (1963,1987)
- Die folgenden
Verteilungen nutzen eine statistische Beschreibung der
Oberflächeneigenschaften.
wobei
Der erste Term ergibt sich aus dem zweiten, wenn man nur das Anfangsglied
der Summe berücksichtigt. Der letzte Term ergibt sich durch eine
Grenzwertbetrachtung der Summe.
Unter Berücksichtigung von
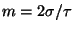 kann der zweite Term
wie folgt umgeschrieben werden:
kann der zweite Term
wie folgt umgeschrieben werden:
- Greenberg und Torrance
- erweitern diese Betrachtungsweise
indem sie einerseits nicht nur
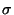 in dieser einfachen Form
betrachten, sondern dieses ebenfalls von den Winkeln abhängig
betrachten, also eine effektive Rauheit beschreiben, und andererseits
den geometrischen Faktor weitergehend analysieren,
so dass sogar Polarisationseigenschaften modelliert werden können.
Wir werden hier allerdings nur die vereinfachte Form angeben, die
für nicht polarisiertes Licht gilt.
in dieser einfachen Form
betrachten, sondern dieses ebenfalls von den Winkeln abhängig
betrachten, also eine effektive Rauheit beschreiben, und andererseits
den geometrischen Faktor weitergehend analysieren,
so dass sogar Polarisationseigenschaften modelliert werden können.
Wir werden hier allerdings nur die vereinfachte Form angeben, die
für nicht polarisiertes Licht gilt.
Der Verteilungsabschwächungsfaktor ist analog dem der zweiten
Gleichung von Beckmann und Bahar 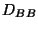 :
:
allerdings wird bei der Berechnung von 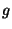
nicht die einfache Beziehung für 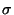 eingesetzt, sondern auch
hier wird eine effektive Rauheit eingesetzt:
eingesetzt, sondern auch
hier wird eine effektive Rauheit eingesetzt:
wobei sich 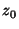 aus der Lösung der Gleichung
aus der Lösung der Gleichung
ergibt. Die beiden Werte 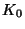 und
und 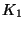 berechnen sich für den
einfallenden und den reflektierenden Vektor als:
berechnen sich für den
einfallenden und den reflektierenden Vektor als:
wobei die 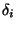 --analog zu oben--die entsprechenden Winkel darstellen.
--analog zu oben--die entsprechenden Winkel darstellen.
Der geometrische Abschwächungsfaktor wird wie folgt angegeben:
hierbei sind die Vektoren 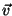 ,
, 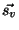 und
und 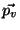
Die beiden anderen Vektoren 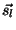 und
und 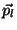 werden analog
mithilfe von
werden analog
mithilfe von 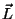 berechnet.
berechnet.




Nächste Seite: Berechnungsmodelle
Aufwärts: Beleuchtungsmodelle hin zur fotorealistischen
Vorherige Seite: Strahlungslehre
Inhalt
© 2004/2005, A. Formella & D. Fellner, Universität Braunschweig
![]() und damit
auch eine geringe Absorptionsrate
und damit
auch eine geringe Absorptionsrate ![]() . Demzufolge ist die Reflexionsrate
. Demzufolge ist die Reflexionsrate
![]() relativ hoch. Es gelten die folgenden Beziehungen:
relativ hoch. Es gelten die folgenden Beziehungen:
![]() mit steigendem Einfallswinkel
mit steigendem Einfallswinkel ![]() , d.h. schaut
man flach auf eine Nicht-Metallplatte, spiegelt sie mehr als bei direkter
Draufsicht.
Die Wellenlängenabhängigkeiten sind deutlich geringer als die der
Metalle. Dies gilt ebenso für die Temperaturabhängigkeit.
Mit anderen Worten, der
Brechungsindex ist annähernd konstant bezüglich
, d.h. schaut
man flach auf eine Nicht-Metallplatte, spiegelt sie mehr als bei direkter
Draufsicht.
Die Wellenlängenabhängigkeiten sind deutlich geringer als die der
Metalle. Dies gilt ebenso für die Temperaturabhängigkeit.
Mit anderen Worten, der
Brechungsindex ist annähernd konstant bezüglich ![]() und
und ![]() .
.
![]() aufgefasst werden.
Für einen Punkt
aufgefasst werden.
Für einen Punkt ![]() gibt
gibt ![]() die Abweichung der
Oberfläche vom Mittelwert an. Es gilt somit:
die Abweichung der
Oberfläche vom Mittelwert an. Es gilt somit:
![]() .
Für die Standardabweichung
.
Für die Standardabweichung ![]() gilt:
gilt:
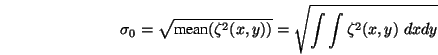

![]() und
und ![]() zum Ausdruck gebracht.
Zum anderen wird
möglicherweise reflektiertes oder einfallendes Licht durch die
Oberfläche selbst
abgeblockt--man könnte Selbstbeschattung sagen, was ebenfalls
die Reflexionsrate reduziert. Dies kann durch einen
Abschwächungsfaktor
zum Ausdruck gebracht.
Zum anderen wird
möglicherweise reflektiertes oder einfallendes Licht durch die
Oberfläche selbst
abgeblockt--man könnte Selbstbeschattung sagen, was ebenfalls
die Reflexionsrate reduziert. Dies kann durch einen
Abschwächungsfaktor ![]() modelliert werden.
modelliert werden.
![]() oft mit
oft mit ![]() bezeichnet, sowie
bezeichnet, sowie
![]() als
als ![]() zusammengefasst.
zusammengefasst.

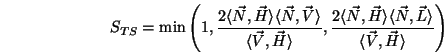
![]() und
und ![]() relativ kompliziert
zu berechnen:
relativ kompliziert
zu berechnen:
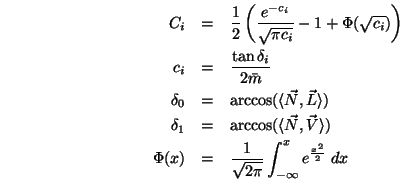
![]() berechnet das Gausssche Fehlerintegral. Dies ist
in mathematischen Bibliotheken (C-Compiler) als erf() enthalten.
Auch die Funktion
berechnet das Gausssche Fehlerintegral. Dies ist
in mathematischen Bibliotheken (C-Compiler) als erf() enthalten.
Auch die Funktion ![]() ist als erfc() vorhanden. Für
den Sancer-Faktor ist eine weitere Materialeigenschaft
ist als erfc() vorhanden. Für
den Sancer-Faktor ist eine weitere Materialeigenschaft
![]() notwendig,
was bei Torrance und Sparrow nicht erforderlich ist.
notwendig,
was bei Torrance und Sparrow nicht erforderlich ist.
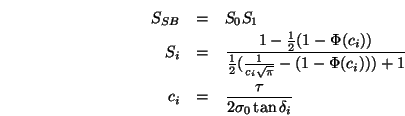
![]() und
und ![]() modelliert werden. Als mögliche Verteilungen wurden die folgenden
vorgeschlagen:
modelliert werden. Als mögliche Verteilungen wurden die folgenden
vorgeschlagen:

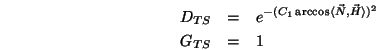
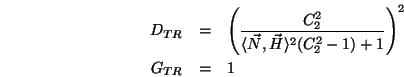
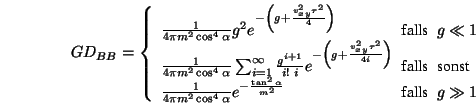
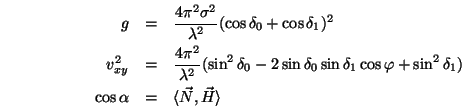
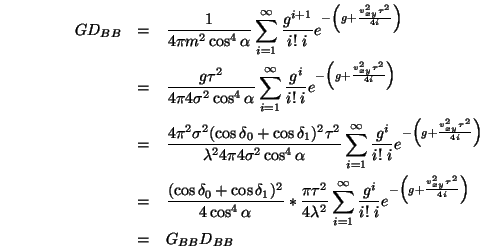
![]() :
: