Man muss zwischen Modell, auch physikalischem Modell, und Gesetz unterscheiden: Modelle sind Erklärungsversuche, z.B. Thesen vor der Ausführung eines physikalischen Experimentes, Gesetze sind Beschreibungen der Realität, die durch Experimente geprüft worden sind und von denen man behaupten kann, dass sie in der Realität gelten; zumindest gibt es keinen Gegenbeweis. Noch nicht in allen Einzelheiten experimentell überprüfte Modelle bezeichnet man auch als Theorien. Modelle gelten meist nur in gewissen Bereichen. Auch Gesetze erlauben Näherungen (z.B. vergleiche klassische Mechanik mit Quantenmechanik).
In der Computergrafik genügen meist Modelle.
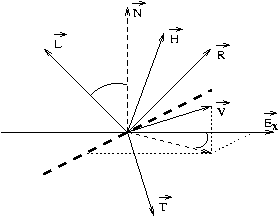
Geometrie an der Objektoberfläche

| Vektoren eines Koordinatensystems | |
| ,,Halbvektor`` zwischen |
|
| Vektor in Richtung einer Lichtquelle | |
| Normalenvektor einer Ebene | |
| Reflexionsvektor an einer Ebene | |
| Transmissionsvektor an einer Ebene | |
| Vektor in Richtung des Betrachters (view) | |
| Polar-,Divergenzwinkel (zwischen |
|
| Azimut, Rotationswinkel (zwischen ,,Vektorebene`` und 1. Koordinatenachse) |
Es gilt je nach betrachtetem Vektor ![]()
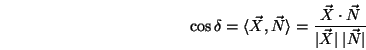
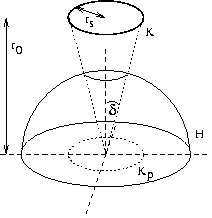
Raumwinkel
wobei ![]() eine Teiloberfläche auf einer Kugel mit Radius
eine Teiloberfläche auf einer Kugel mit Radius ![]() ist,
die durch den betrachteten Winkels aufgespannt wird
(
ist,
die durch den betrachteten Winkels aufgespannt wird
(
![]() entspricht der gesamten Kugel),
entspricht Bogenmaß im Zweidimensionalen.
entspricht der gesamten Kugel),
entspricht Bogenmaß im Zweidimensionalen.
Um den Raumwinkel unabhängig von einem Radius ![]() zu machen, betrachten
wir ein durch
zu machen, betrachten
wir ein durch ![]() und
und ![]() aufgespanntes Koordinatensystem, d.h. die Menge
aufgespanntes Koordinatensystem, d.h. die Menge
Für einen differentiellen Raumwinkel ![]() gilt dann:
gilt dann:
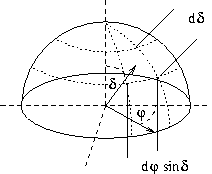
Den Raumwinkel einer Halbkugel erhält man damit als
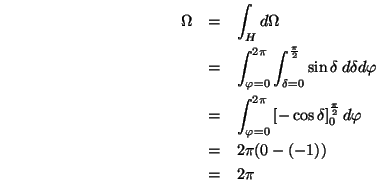
Raumwinkelberechnung einer Kreisscheibe
Integriert man nicht über den gesamten Halbraum bezüglich ![]() , d.h. man betrachtet nur einen Teilwinkel, der sich z.B. als Projektion einer
Kreisscheibe
, d.h. man betrachtet nur einen Teilwinkel, der sich z.B. als Projektion einer
Kreisscheibe ![]() auf die Hemisphere ergibt, erhält man
auf die Hemisphere ergibt, erhält man
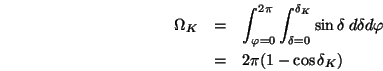
Betrachte Kreisscheibe ![]() mit Radius
mit Radius ![]() im Abstand
im Abstand ![]() vom
Beobachtungspunkt; die Projektion auf die Einheitskugel liefert
Polarwinkel
vom
Beobachtungspunkt; die Projektion auf die Einheitskugel liefert
Polarwinkel ![]()
Liegt nun die Kreisscheibe weit vom Beobachtungspunkt entfernt, d.h. ![]() ist wesentlich größer als
ist wesentlich größer als ![]() , kann man die Näherung
, kann man die Näherung

Nun ist aber ![]() gerade die Fläche der betrachteten Kreisscheibe,
d.h. man kann kleine Raumwinkel, die sich als Projektion einer Fläche
gerade die Fläche der betrachteten Kreisscheibe,
d.h. man kann kleine Raumwinkel, die sich als Projektion einer Fläche ![]() ergeben, durch die Projektionsfläche in der Betrachterebene dividiert
durch den quadratischen Abstand annähern:
ergeben, durch die Projektionsfläche in der Betrachterebene dividiert
durch den quadratischen Abstand annähern:
Diese Näherung wird bei der sogenannten Radiosity-Methode verwendet.
Man kann folgende Strahlungsarten mit den entsprechenden Koeffizienten unterscheiden, dabei bedeutet ein dicker Pfeil gerichtete Strahlung und dünne Pfeile diffuse Strahlung.
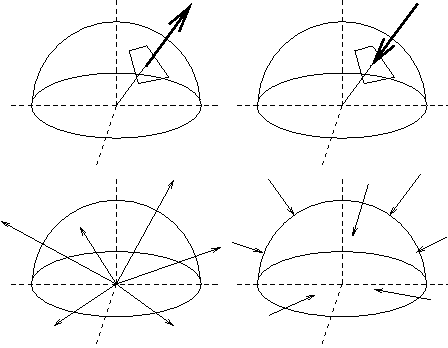
| gerichtete Emmisionsrate | directional emissivity | |
| diffuse Emmisionsrate | hemisperical emissivity | |
| gerichtete Absorptionsrate | directional absorptivity | |
| diffuse Absorptionsrate | hemisperical absorptivity |
| gerichtete Reflexionsrate bei gerichteter Immision | bidirectional spectral reflectivity | |
| gerichtete Reflexionsrate bei diffuser Immision | directional-hemispherical reflectivity | |
| diffuse Reflexionsrate bei gerichteter Immision | hemispherical-directional reflectivity | |
| diffuse Reflexionsrate bei diffuser Immision | hemispherical reflectivity |
Wie die einzelnen Koeffizienten berechnet werden und welche in der Computergrafik eine Rolle spielen, sehen wir in den folgenden Ausführungen.
Die Strahlungsstärke ist eine Eigenschaft des Strahlers und
unabhängig von der Entfernung eines möglichen Beobachters.
Ist ![]() konstant, handelt es sich um einen isotropen Strahler,
der in alle Richtungen die gleiche Strahlungsleistung abgibt.
Es gilt dann:
konstant, handelt es sich um einen isotropen Strahler,
der in alle Richtungen die gleiche Strahlungsleistung abgibt.
Es gilt dann:
Isotrope Strahler kommen jedoch kaum vor, da Strahler eine Geometrie
besitzen und jedes Flächenstück ![]() des Strahlers einen Teil zur
Gesamtstrahlungsleistung
des Strahlers einen Teil zur
Gesamtstrahlungsleistung ![]() beiträgt
(in großen Entfernungen können jedoch auch nicht-isotrope Strahler
als isotrope Strahler modelliert werden, z.B. Sonnenlicht oder
vereinfachte Punktlichtquellen)
beiträgt
(in großen Entfernungen können jedoch auch nicht-isotrope Strahler
als isotrope Strahler modelliert werden, z.B. Sonnenlicht oder
vereinfachte Punktlichtquellen)
Gilt nun, dass die Strahlungsstärke eines Flächenstücks ![]() nur von der Beobachtungsrichtung
nur von der Beobachtungsrichtung
![]() gemäß
gemäß
Die Strahlungsleistung des gesamten Flächenstücks (in einen Halbraum) beträgt dann
![\begin{eqnarray*}
\Phi&=& \int_H J(\delta)\;d\Omega \\
&=& \int_H B\;dS\cos\de...
...ft[\frac{1}{2}\sin^2\delta\right]^{\pi/2}_{0} \\
&=&\pi\;dS\;B
\end{eqnarray*}](img461.gif)
Herrscht auf einem Flächenstück ![]() der Strahlungsfluss
der Strahlungsfluss ![]() ,
bezeichnet
,
bezeichnet ![]() die Intensität (Strahlungsflussdichte) auf dem
Flächenstück mit
die Intensität (Strahlungsflussdichte) auf dem
Flächenstück mit
Oder anders:
Den Gesamtfluss, der auf einer Fläche herrscht, erhält man als
Oberflächenintegral
Analog kann man die spezifische Ausstrahlung ![]() (oder Intensität des
Strahlers) definieren,
die die von einem Oberflächenstück
(oder Intensität des
Strahlers) definieren,
die die von einem Oberflächenstück ![]() abgegebene Strahlungsleistung
spezifiziert.
abgegebene Strahlungsleistung
spezifiziert.
Nochmal:
Betrachten wir einen Strahler, der ein Flächenstück ![]() aus einem Raumwinkel
aus einem Raumwinkel ![]() von hinreichend weiter Entfernung
beleuchtet. Dieses erscheint dem Strahler als Raumwinkel
von hinreichend weiter Entfernung
beleuchtet. Dieses erscheint dem Strahler als Raumwinkel
Nehmen wir nun an, dass die Strahlungsstärke ![]() des Strahlers
in dem Bereich annähernd konstant ist, folgt für den
Strahlungsfluss bezüglich des Flächenstücks
des Strahlers
in dem Bereich annähernd konstant ist, folgt für den
Strahlungsfluss bezüglich des Flächenstücks ![]()
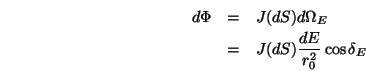
Wir erhalten also für den Strahlungsfluss der Fläche ![]()
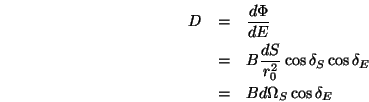
Fassen wir nochmals die Bedingungen für die Näherungen zusammen:
Obige Gleichungen sind eigentlich auch von der Wellenlänge abhängig, d.h. vorallem die Intensität steht mit der Wellenlänge in Zusammenhang.
Das Lambertsche Gesetz wurde schon bei der Interaktion zwischen Strahler und bestrahlter Fläche erläutert. Es besagt, das die Intensität bzw. die Strahlungsstärke nur vom Kosinus des Betrachtungswinkels abhängt.
Es gilt einerseits das Reflexionsgesetz:
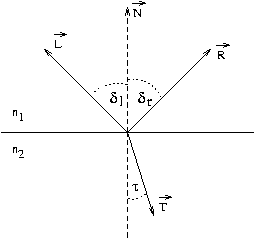
Die Brechungsindizes sind von der Wellenlänge abhängig, d.h. man
muss das Gesetz mit ![]() formulieren. Sind die Materialien nicht
isotrop bezüglich der elektromagnetischen Eigenschaften, ist der
Brechungsindex sogar komplex, d.h. abhängig von
formulieren. Sind die Materialien nicht
isotrop bezüglich der elektromagnetischen Eigenschaften, ist der
Brechungsindex sogar komplex, d.h. abhängig von ![]() .
.
Ab einem gewissen Eintrittswinkel tritt Totalreflexion auf, d.h. der Strahl aus dem dichteren Medium (größerer Brechungsindex) kann nicht mehr in das dünnere Medium eindringen.
Dies tritt genau dann ein, wenn für den Eintrittswinkel ![]() gilt:
gilt:
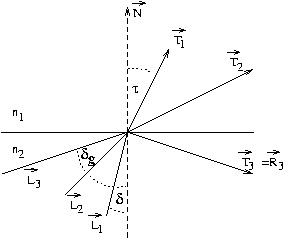
Die Fresnelschen Gleichungen sind speziell für die Modellierung von Metallen wichtig:
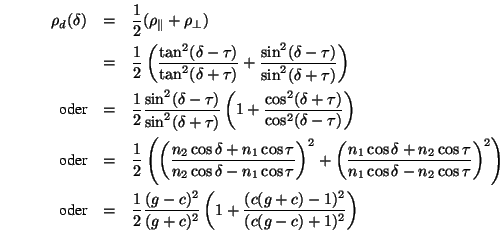
Wobei für die letzte Zeile gilt:
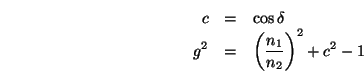
![]() ist natürlich von der Wellenlänge abhängig, da der
Brechungsindex von dieser abhängt. Der Zusammenhang zwischen
ist natürlich von der Wellenlänge abhängig, da der
Brechungsindex von dieser abhängt. Der Zusammenhang zwischen ![]() und
und ![]() ist über das Snellsche Gesetz gegeben. In der
zweiten ``oder''-Gleichung wird der Winkel
ist über das Snellsche Gesetz gegeben. In der
zweiten ``oder''-Gleichung wird der Winkel ![]() im Gegensatz zur
bisherigen Definition auch gegen den Normalenvektor gemessen, der
Winkel ist also größer als 90 Grad. Im andern Fall muss das
Vorzeichen von
im Gegensatz zur
bisherigen Definition auch gegen den Normalenvektor gemessen, der
Winkel ist also größer als 90 Grad. Im andern Fall muss das
Vorzeichen von ![]() negiert werden.
negiert werden.
Als Spezialfälle erhält man:
Ist das dünnere Medium Luft, vereinfacht sich die Gleichung weiter zu
Hat man den Brechungsindex ![]() in Abhängigkeit von der Wellenlänge
gegeben, kann man
in Abhängigkeit von der Wellenlänge
gegeben, kann man ![]() bestimmen. Sind Messwerte für
bestimmen. Sind Messwerte für ![]() vorhanden, kann man damit erst den Brechungsindex des Materials bestimmen
und daraus schließlich
vorhanden, kann man damit erst den Brechungsindex des Materials bestimmen
und daraus schließlich ![]() berechnen.
berechnen.
Das Snellsche Gesetz und die Fresnelschen Gleichungen sind
hier nur für den Fall von isotropen Medien angegeben. Handelt es sich
um ein Material mit komplexem Brechungsindex, d.h. senkrecht und parallel
zur Grenzfläche verlaufende Wellenanteile werden unterschiedlich
gebrochen bzw. transmittiert, ergeben sich komplexe Ausdrücke.
Diese lauten für den einfachen Fall, dass aus einem Medium mit reellem
Brechungsindex ![]() (Luft) eine Welle auf ein Medium mit komplexem
Brechungsindex
(Luft) eine Welle auf ein Medium mit komplexem
Brechungsindex ![]() trifft (
trifft (![]() heißt auch
Extinktionskoeffizient):
heißt auch
Extinktionskoeffizient):
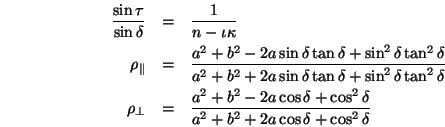
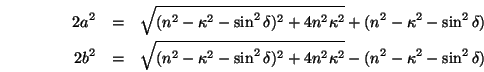
Der Reflexionskoeffizient ergibt sich bei unpolarisiert einfallendem
Licht analog zu oben als Mittelwert der beiden Werte ![]() und
und
![]() .
.
Ist das Verhältnis ![]() kann weiter genähert werden:
kann weiter genähert werden:
Im Folgenden wird der Reflexionskoeffizient aufgrund der
Fresnelschen Gleichungen mit ![]() abgekürzt.
abgekürzt.