Funciones de Fourier

asumimos por el momento que exista una base ortonormal $(\varphi_k)_{k\in J}$ de un espacio de funciones con $J$ adecuadamente, p.ej., las funciones de Fourier para las funciones $T$-periódicas:

una función $f$ es $T$-periódica si $f(t)=f(t+T)$ para todos los $t$

$\omega\in\bbbr^+$, $T=2\pi/\omega$: $\sin(\omega t)$ y $\cos(\omega t)$ son $T$-periódicas

sea $f$ una función $T$-periódica sobre $\bbbr$ y $\omega=2\pi/T$

$$f(t)=a_0/2+\sum_{k=1}^{\infty}a_k\cos(k\omega t)+b_k\sin(k\omega t)$$

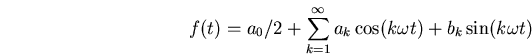
con los coeficientes de Fourier

$$\begin{eqnarray*} a_k &=& 2/T\int_0^T f(t)\cos(k\omega t) dt \qquad k=0,1,2,\do... ...2,\dots \\ &=& 2/T\langle f(\cdot),\sin(k\omega\cdot)\rangle \end{eqnarray*}$$

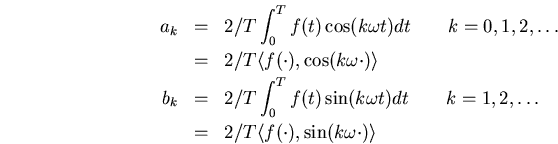
donde usamos la notación que aplican los matemáticos muy amenudo: $f(\cdot)$ el la función $f$ para todos sus argumentos permitidos

las funciones $1,\cos(\omega t),\cos(2\omega t),\cos(3\omega t),\dots, \sin(\omega t),\sin(2\omega t),\sin(3\omega t),\dots$ son una base ortogonal del espacio de funciones $L^2(T)$

ortogonal, porque para todos los $k,m\in\bbbn$

$$\begin{eqnarray*} \langle\cos(k\omega t),\cos(m\omega t)\rangle _T &=& \int_0... ...gle _T &=& \int_0^T\cos(k\omega t)\sin(m\omega t)dt\\ &=& 0 \end{eqnarray*}$$

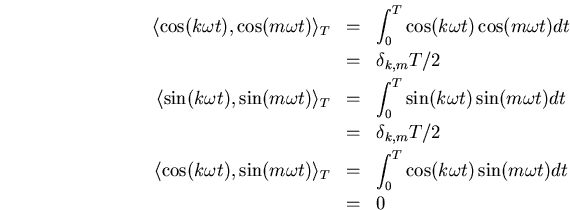
``justificación'' gráfica:

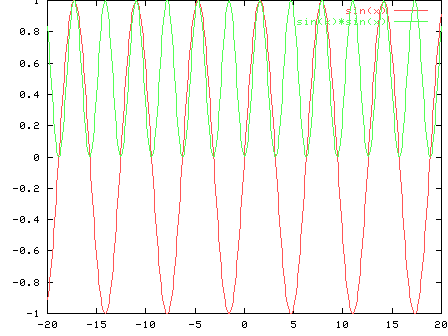
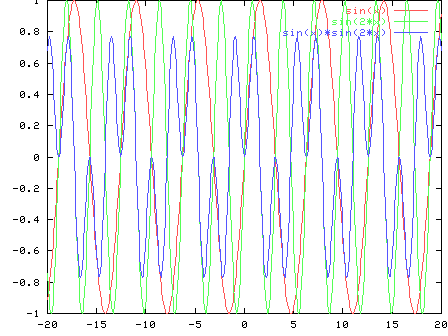
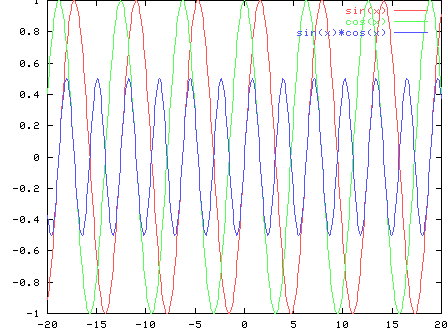
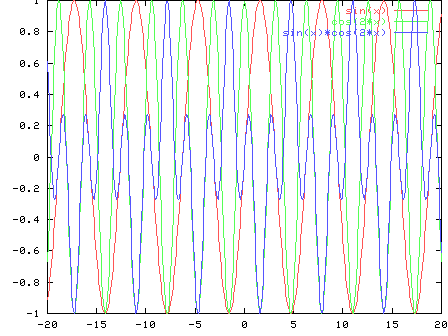
la secuencia de Fourier converge en los puntos de discontinuidad de la función al valor medio entre el límite derecho y el límite izquierdo

ejemplo:

la función original es una función $T$-periódica con $T=2\pi$ de forma de sierra siendo sobre el intervalo $[0:2\pi)$

$$s_T(x)=\frac{\pi-x}{2} \qquad 0\leq x < 2\pi$$

la combinación lineal con funciones bases de Fourier es

$$s(x)=\sum_{k=1}^\infty \frac{1}{k}\sin(kx)$$

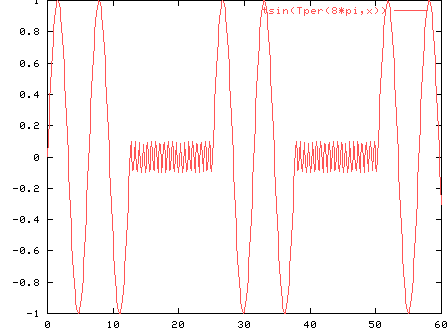
la gráfica representa la función original y su aproximación con la secuencia cortada después de $k=8$

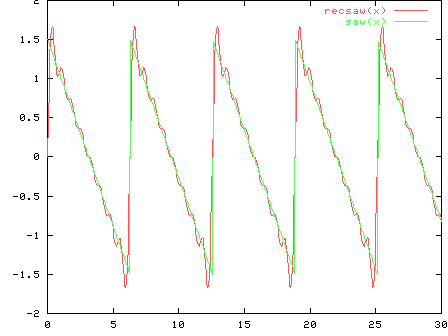
el fenómeno que la aproximación oczila alrededor de la función original y con más amplitud cerca de los puntos de discontinuidad se llama fenómeno de Gibbs y aparece en muchos casos de aproximaciones