Projecciones ortogonales

sea $(\varphi_k)_{k\in J}$ un sistema de funciones en ${\rm L}^2(\bbbr)$ (no necesariamente una base!)

las funciones $(\varphi_k)_{k\in J}$ generan, construyendo con composiciones lineales, un subespacio en ${\rm L}^2(\bbbr)$ es decir, solamente una parte de todas las funciones posibles

p.ej.

$$\begin{eqnarray*} \varphi(x) &=& \left\{\begin{array}{l@{\quad;\quad}c} 1 & 0... ...ay}\right. \\ \varphi_k(x) &=& \varphi(x-k) \qquad k\in\bbbz \end{eqnarray*}$$

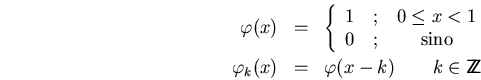
es decir, tenemos un número infinito (pero contable) de funciones de tipo

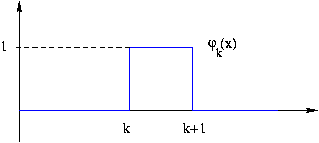
$(\varphi_k)_{k\in \bbbz}$ es obviamente ortonormal (las cajas no se solapan y la integral es 1)

con los $(\varphi_k)_{k\in \bbbz}$ podemos construir cualquier función de escalones en ${\rm L}^2(\bbbr)$, que son constantes en todos los intervalos $[k,k+1)$

pregunta interesante: cuáles de las funciones que podemos generar con $(\varphi_k)_{k\in J}$ aproxima una función $f$ de ${\rm L}^2(\bbbr)$ lo mejor?

es decir, buscamos coeficientes $(c_k)_{k\in J}$ de la combinación lineal así que

$$\Vert\sum_{k\in J} c_k \varphi_k - f \Vert \qquad\mbox{sea m\'{\i}nima}$$

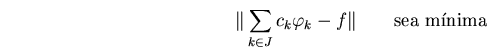
si el sistema de funciones es ortonormal la respuesta es fácil

$$\begin{eqnarray*} \lefteqn{\Vert\sum_{k\in J} c_k \varphi_k - f \Vert^2}\\ &=... ...t\sum_{k\in J} c_k\langle\varphi_k,f\rangle +\langle f,f\rangle \end{eqnarray*}$$

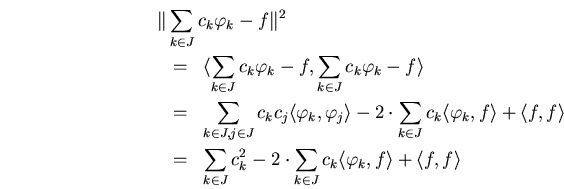
para el mínimo todas las derivadas parciales respeto a todo los $c_k$ tienen que desvanecer, es decir

$$2c_k-2\cdot\langle\varphi_k,f\rangle = 0$$

entonces

$$c_k=\langle\varphi_k,f\rangle$$

es decir, la mejor aproximación de la función $f$ a base del sistema de funciones $(\varphi_k)_{k\in J}$ (dentro de ${\rm L}^2(\bbbr)$ y con la norma $L_2$) es la llamada proyección ortogonal

$$Pf = \sum_{k\in J}\langle\varphi_k,f\rangle \varphi_k$$

retomamos el ejemplo de las funciones de cajas $(\varphi_k)_{k\in \bbbz}$:

$$\begin{eqnarray*} c_k &=& \langle\varphi_k,f\rangle \\ &=& \int_\bbbr \varphi_k(x)f(x)dx\\ &=& \int_k^{k+1}f(x)dx \end{eqnarray*}$$

una razón porque el cálculo es tan fácil es que las $\varphi_k$ tienen soporte compacto

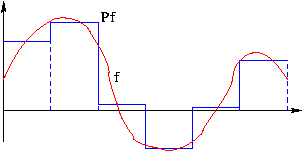
Por qué necesitamos eso?

p.ej. si comprimimos datos con perdidas queremos minimizar dichas perdidas.

arriba hemos comprobado que la aproximación con los coeficientes $c_k=\langle\varphi_k,f\rangle$ es la mejor basada en las funciones de cajas, sin embargo, el error de aproximación

$$\epsilon=\Vert\sum_{k\in J} c_k \varphi_k - f \Vert\geq 0$$

siempre es major que 0 mientras $f$ no sea una función de escalones adecuadas.

observamos que la elección de funciones de cajas sobre un intervalo de anchura 1 no es la única manera de hacerlo: cualquier sistema de funciones de cajas valdría para realizar una aproximación más o menos cerca

especialmiente podemos usar funciones de cajas de anchura $2^{-j}$ (para algún $j\in\bbbz$) y altura $2^j$ para que sean normalizadas, entonces

$$\begin{eqnarray*} c_k &=& \langle\varphi_k,f\rangle \\ &=& \int_\bbbr \varphi_k(x)f(x)dx\\ &=& 2^j\int_{k2^{-j}}^{(k+1)2^{-j}}f(x)dx \end{eqnarray*}$$

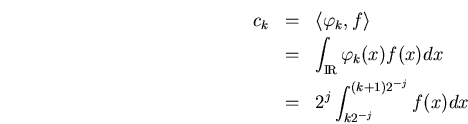
llamamos una aproximación de una función $f$ en forma de escalones (con funciones de cajas de anchura $2^{-j}$) $E^jf$, es decir, con $j$ suficientemente grande, tenemos

$$f \approx E^jf$$