


Next: Funciones de Fourier
Up: Sistemas de funciones ortogonales
Previous: Algebra con funciones
retomamos la representación de 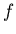 de antes:
de antes:
donde
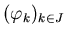 es una colección de funciones indizadas
con índices tomados del conjunto
es una colección de funciones indizadas
con índices tomados del conjunto 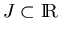 (finito o infinito)
(finito o infinito)
calcular los coeficientes 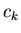 es fácil (ya lo vimos) si los
es fácil (ya lo vimos) si los
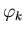 forman un sistema ortonormal de funciones, es decir
forman un sistema ortonormal de funciones, es decir
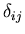 se llama símbolo de Kronecker
se llama símbolo de Kronecker
o bien
si
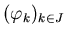 sólo es ortogonal (pero no ortonormal)
tenemos
sólo es ortogonal (pero no ortonormal)
tenemos
entonces tenemos como respuestas a las tres preguntas
- Cómo se calcula los
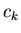 (dados los
(dados los 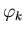 y
y 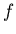 )?
)?
con la fórmula arriba
- Son los coeficientes
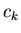 únicos?
únicos?
si
- Cuáles de las posibles funciones
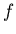 se puede representar de
tal forma?
se puede representar de
tal forma?
clases de teoría de funciones, las funciones que vamos
a encontrar en la práctica suelen caer en dicha clase



Next: Funciones de Fourier
Up: Sistemas de funciones ortogonales
Previous: Algebra con funciones
© 2002, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() de antes:
de antes:
![]() es una colección de funciones indizadas
con índices tomados del conjunto
es una colección de funciones indizadas
con índices tomados del conjunto ![]() (finito o infinito)
(finito o infinito)
![]() es fácil (ya lo vimos) si los
es fácil (ya lo vimos) si los
![]() forman un sistema ortonormal de funciones, es decir
forman un sistema ortonormal de funciones, es decir
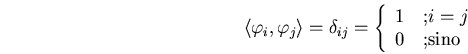
![]() se llama símbolo de Kronecker
se llama símbolo de Kronecker
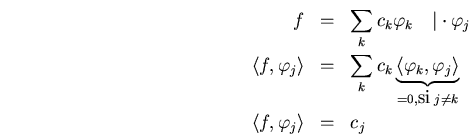
![]() sólo es ortogonal (pero no ortonormal)
tenemos
sólo es ortogonal (pero no ortonormal)
tenemos
