Algebra con funciones

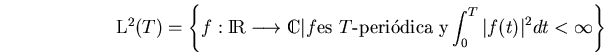
vamos a los espacios de funciones, en especial:

• ${\rm L}^2(\bbbr)$ conjunto de funciones de ``energia limitada''

  
  

  $$\mbox{${\rm L}^2(\bbbr)$}=\left\{f:\bbbr\longrightarrow \bbbc\vert\int_\bbbr\vert f(t)\vert^2dt<\infty\right\}$$
  
  

• ${\rm L}^2(T)$ conjunto de funciones $T$-periódicas (es decir, $f(t)=f(t-T)$ para para todos los $t$)

  
  

  $$\mbox{${\rm L}^2(T)$}=\left\{f:\bbbr\longrightarrow \bbbc\ver... ...$T$-peri\'odica y} \int_0^T\vert f(t)\vert^2dt<\infty\right\}$$
  
  

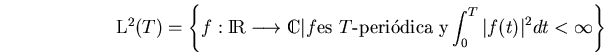
usamos como productos escalares en estos espacios:

$$\langle f,g\rangle =\int_\bbbr f(t)\overline{g(t)}dt \qquad f,g\in \mbox{${\rm L}^2(\bbbr)$}$$

$$\langle f,g\rangle _T=\int_0^T f(t)\overline{g(t)}dt \qquad f,g\in \mbox{${\rm L}^2(T)$}$$

el complejo conjugado garantiza que la integral se calcula en $\bbbr$

la norma (``longitud de vectores'') calculamos entonces como:

$$\Vert f\Vert=\sqrt{\langle f,f\rangle }$$

$$\Vert f\Vert _T=\sqrt{\langle f,f\rangle _T}$$

como consecuencia tenemos

$$f\in\mbox{${\rm L}^2(\bbbr)$}\qquad\mbox{$\Longrightarrow$}\q... ...ghtarrow \infty \mbox{\quad o\quad} t\longrightarrow \-\infty$$

podemos usar la norma de la diferencia de dos funciones para medir el grado de aproximación entre ellas, $\Vert f-g\Vert$

todo eso ya hemos hecho y usado anteriormente