repetimos un poco de álgebra con vectores en el plano (espacio vectorial de dimensión 2)
si dos vectores ![]() y
y ![]() son linealmente independiente podemos
escribir cualquier vector
son linealmente independiente podemos
escribir cualquier vector ![]() como
como
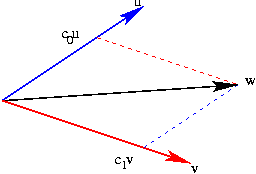
si los vectores están dados dentro de un sistema de coordenadas ortonormal, tenemos
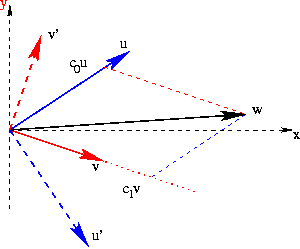
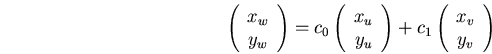
calculamos ![]() y
y ![]() a base de este sistema lineal
a base de este sistema lineal
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
con
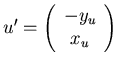 |
con
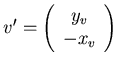 |
|
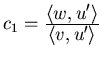 |
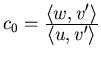 |
si ![]() perpendicular a
perpendicular a ![]() (
(![]() ), es decir,
), es decir,
![]() y
y
![]() tenemos:
tenemos:
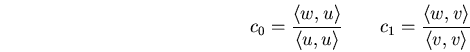
se puede derivar también directo:

si adicionalmente
![]() , es decir, los vectores
son normalizados, calcular los coeficientes es fácil:
, es decir, los vectores
son normalizados, calcular los coeficientes es fácil:
es decir