Schnittpunkt von Segmenten bzw. Strahl und Segment

Erste Methode

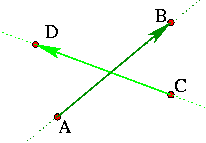
Parametrische Form der beiden Geraden:

$$\begin{eqnarray*} P(t) &=& A + t\cdot(B-A) = A + tX \\ P(s) &=& C + s\cdot(D-C) = C + sY \end{eqnarray*}$$

Setzen $P(t)=P(s)$ und bestimmen $s$ und $t$:

$$\begin{eqnarray*} P(t) &=& P(s) \\ A + tX &=& C + sY \\ tX &=& C-A +sY \end{eqnarray*}$$

oder als Koordinatengleichungen:

$$\begin{eqnarray*} tx_0 &=& (c_0-a_0)+sy_0 \\ tx_1 &=& (c_1-a_1)+sy_1 \end{eqnarray*}$$

Wir können dies direkt mit der Kramerschen Regel berechnen, wollen hier aber nochmal den Weg angeben.

Eliminieren von $t$ und weiteres Umformen:

$$\begin{eqnarray*} ((c_1-a_1)+sy_1)/x_1&=&((c_0-a_0)+sy_0)/x_0\\ &&\\ x_0\cdot(... ...ay}{cc}(c_0-a_0) & x_0\\ (c_1-a_1) & x_1\end{array}\right\vert \end{eqnarray*}$$

Ist die Determinate der beiden Spaltenvektoren X und Y ungleich 0; erhalten wir:

$$\begin{eqnarray*} s&=& \frac{ \left\vert\begin{array}{cc}(c_0-a_0) & x_0\\ (c_... ...}b_0-a_0 & d_0-c_0\\ b_1-a_1 & d_1-c_1\end{array}\right\vert } \end{eqnarray*}$$

und in analogerweise bei Elimination von $s$:

$$sY = A-C +tX$$

d.h. vertausche $X$ mit $Y$ und $A$ mit $C$, also

$$\begin{eqnarray*} t&=& \frac{ \left\vert\begin{array}{cc}(a_0-c_0) & y_0\\ (a_... ...}c_0-d_0 & b_0-a_0\\ c_1-d_1 & b_1-a_1\end{array}\right\vert } \end{eqnarray*}$$

Damit sich die Segmente (nicht nur die Geraden) schneiden, muss außerdem gelten:

$$\begin{eqnarray*} 0\leq s \leq 1 \\ 0\leq t \leq 1 \end{eqnarray*}$$

Ist die Determinante gleich 0, so sind die beiden Geraden der Segmente parallel oder sogar identisch.

Wie unterscheidet man die beiden Fälle? Übung!

Zweite Methode

secintersectImplizite Form der Geraden des einen Segments

$$(x-a_0)(b_1-a_1)-(y-a_1)(b_0-a_0)=0$$

parametrisierte Form der Geraden des anderen Segments

$$\begin{eqnarray*} x(s)&=&c_0+s\cdot(d_0-c_0)\\ y(s)&=&c_1+s\cdot(d_1-c_1) \end{eqnarray*}$$

Einsetzen der parametrisierten Gleichungen in die implizite Gleichung

$$(c_0-a_0+s\cdot(d_0-c_0))(b_1-a_1)-(c_1-a_1+s\cdot(d_1-c_1))(b_0-a_0)=0$$

und umformen:

$$\begin{eqnarray*} \lefteqn{s\cdot[(d_0-c_0)(b_1-a_1)-(d_1-c_1)(b_0-a_0)]}\\ &=& (c_1-a_1)(b_0-a_0)-(c_0-a_0)(b_1-a_1) \end{eqnarray*}$$

und somit mit Determinaten

$$\begin{eqnarray*} s\cdot\left\vert\begin{array}{cc}d_0-c_0 & b_0-a_0\\ d_1-c_1... ...cc}a_0-b_0 & c_0-a_0\\ a_1-b_1 & c_1-a_1\end{array}\right\vert \end{eqnarray*}$$

Und es ergeben sich die gleichen Resultate wie bei der ersten Methode (durch entsprechendes Umformen der Determinanten):

$$\begin{eqnarray*} s&=&\frac{\left\vert\begin{array}{cc}a_0-b_0 & c_0-a_0\\ a_1... ...c}d_0-c_0 & b_0-a_0\\ d_1-c_1 & b_1-a_1\end{array}\right\vert} \end{eqnarray*}$$

und analogerweise

$$\begin{eqnarray*} t&=&\frac{\left\vert\begin{array}{cc}d_0-c_0 & c_0-a_0\\ d_1... ...c}d_0-c_0 & b_0-a_0\\ d_1-c_1 & b_1-a_1\end{array}\right\vert} \end{eqnarray*}$$

Auch hier überprüft man

$$\begin{eqnarray*} 0\leq s \leq 1 \\ 0\leq t \leq 1 \end{eqnarray*}$$

Schnittpunkt zwischen Segment und Strahl ist einfach: man überprüft auf entsprechend positiven Parameterwert!

Dritte Methode

Wir machen uns die Orientierung zunutze (wobei wir aber keine Information über den konkreten Schnittpunkt erhalten):

bool Intersect(point A, point B, point C, point D) {
  return
    Orientation(A,B,C)!=Orientation(A,B,D) &&
    Orientation(C,D,A)!=Orientation(C,D,B);
}

Man sollte jedoch die Spezialfälle beachten (insbesondere liefert obige Funktion nicht das erwartete Ergebnis, wenn alle vier Punkte auf einer Geraden liegen: nämlich immer kein Schnittpunkt, obwohl sich die Segmente überlappen könnten).

Besser ist:

int Intersect(point A, point B, point C, point D) {
  int abc(Orientation(A,B,C));
  int abd(Orientation(A,B,D));
  int cda(Orientation(C,D,A));
  int cdb(Orientation(C,D,B));

  if( abc!=abd && cda!=cdb ) return intersect;
  if( abc==0 && abd==0 && cda==0 && cdb==0 ) return collinear;
  return nointersect;
}

Den kollinearen Fall kann man dann durch lexikografischen Vergleich der vier Punkte lösen, falls notwendig.