Orientierung

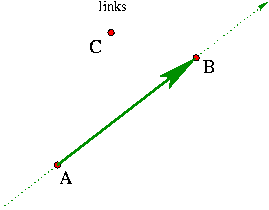
von drei Punkten bzw. von einem Punkt und einem Segment

$C$ liegt links, wenn wir von $A$ nach $B$ gehen.

Oder, wenn wir entlang den Kanten des Polygons von $A$ nach $B$ nach $C$ und wieder nach $A$ gehen, so laufen wir eine Runde entgegen dem Uhrzeigersinn.

Wir können das Kreuzprodukt 3-dimensionaler Vektoren bemühen, wir setzen die dritte Komponente null, also $A_2=B_2=C_2=0$:

$$\left(\begin{array}{c}N_0\\ N_1\\ N_2\end{array}\right) = \... ...left(\begin{array}{c}A_0\\ A_1\\ A_2\end{array}\right) \right)$$

d.h. $N$ steht sowohl senkrecht auf dem Vektor $B-A$ als auch auf dem Vektor $C-A$ und fungiert als Drehachse um $B-A$ über den kleineren Winkel in Richtung $C-A$ zu drehen.

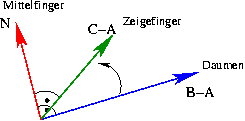
Rechte-Hand-Drei-Finger-Regel: Daumen in Richtung $B-A$, Zeigefinger in Richtung $C-A$, dann zeigt der Mittelfinger in Richtung $N$.

$$\begin{eqnarray*} \left(\begin{array}{c}N_0\\ N_1\\ N_2\end{array}\right) &=& ... ...0 \\ (B_0-A_0)(C_1-A_1)-(B_1-A_1)(C_0-A_0) \end{array}\right) \end{eqnarray*}$$

also ist

$$N_2= (B_0-A_0)(C_1-A_1)-(B_1-A_1)(C_0-A_0)$$

• positiv, so liegt $C$ links,
• negativ, so liegt $C$ rechts,
• null, so liegt $C$ auf der duch $A$ und $B$ definierten Gerade

Wir können auch Determinantenschreibweise verwenden:

$$N_2= \left\vert\begin{array}{cc}B_0-A_0 & C_0-A_0\\ B_1-A_1 & C_1-A_1\end{array}\right\vert$$

Wir können auch über die Fläche des Dreiecks $ABC$ argumentieren, hierzu schreiben wir:

$$A={x_0 \choose y_0} \qquad B={x_1 \choose y_1} \qquad C={x_2 \choose y_2}$$

und mithilfe folgender Zeichnung

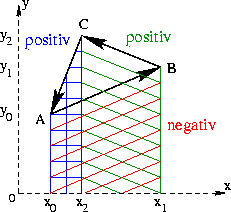
areatriangleberechnen wir die orientierte Fläche durch vorzeichenrichtiges Addieren der Trapeze zu:

$$\begin{eqnarray*} a&=& \frac{1}{2}(y_2+y_0)(x_2-x_0)+ \frac{1}{2}(y_1+y_2)(x_... ...y_0+ x_1y_1+x_1y_2-x_2y_1-x_2y_2+ x_0y_1+x_0y_0-x_1y_1-x_1y_0) \end{eqnarray*}$$

und wir erhalten:

$$a=\frac{1}{2}\sum_{i=0}^2 (x_iy_{i+1}-x_{i+1}y_i)$$

wobei wir den Index $i$ in der Summe modulo 3 bilden, d.h. $x_3=x_0$ und $y_3=y_0$.

Ist das Dreieck im Uhrzeigersinn orientiert, ergibt sich eine negative Fläche.

Rechnen Sie nach, dass $N_2=2a$ ist! Übung

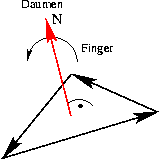
Rechte-Hand-Umlauf-Regel: Zeigen die Finger der rechten Hand in Umlaufrichtung der Punktordnung, so zeigt der Daumen in Richtung des Normalenvektors.

Wir können also eine Funktion schreiben:

int Orientation(A,B,C)

die einen von drei möglichen Werten zurückliefert (man nimmt üblicherweise -1 für rechts, 0 für auf, und 1 für links).