Anpassung an Ausgabegeräte

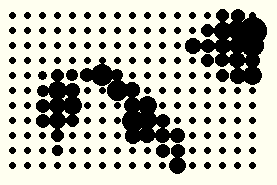
Steht bei einem Ausgabegerät

• nur eine geringe Anzahl von Intensitätswerten/Farbwerten pro Pixel zur Verfügung,
• will man aber ein Bild mit vielen Werten darstellen,

so versucht man durch

• spezielle Wahl der Intensitäten/Farben
• benachbarter Pixel
• beim Betrachter den subjektiven Eindruck

von mehr Werten zu erzeugen.

Schwarz/Weiß/Grau-Bilder

Halftoning

Klassisches halftoning nutzt schwarze Kreisscheiben mit Zentren auf einem regelmäßigen Raster und kontinuierlich einstellbarem Radius um viele Grauwerte zu erzeugen (Zeitungsdruck).

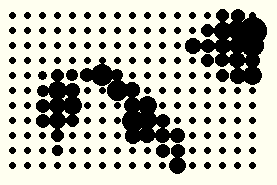
Für Rastergrafikgeräte kann man einen ähnlichen Effekt erzeugen:

Idee: nutze Pixelmuster zur Darstellung von Intensitätswerten oder Farbwerten.

Man fasst rechteckige Bereiche von Pixeln zusammen und setzt in diesem Bereich eine bestimmte Anzahl von Pixeln, um so einen entsprechenden Grauwert zu erhalten:

Für quadratische Bereiche mit einer Kantenlänge von $n$ Pixeln stehen also $n^2+1$ viele Werte zur Verfügung.

Beim Besetzen der Bereiche sollte man darauf achten, dass keine regelmäßigen Muster mit vorherrschenden Linien entstehen, d.h. folgende Muster sind z.B. möglichst zu vermeiden

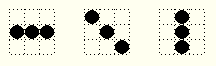
Natürlich kann man das Verfahren auch anwenden, wenn mehr als eine Intensitätsstufe pro Pixel zur Verfügung steht:

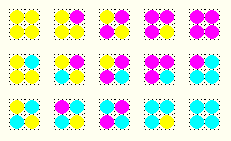
oder wenn mehr als eine Farbe pro Pixel darstellbar ist (Beispiel):

Eigenschaften:

• $n^2+1$ viele Intensitätsstufen bei Pixelmustern mit quadratischen Bereichen der Kantenlänge $n$
• dabei Veränderung der Auflösung um Faktor $n$

Ohne Veränderung der Auflösung kommt Dithering aus.

Dithering

Idee: Kachele das Orginalbild mit einer ``kleinen'' Dithermatrix und setze in der Darstellung nur dann ein Pixel, wenn der Originalwert größergleich dem Matrixeintrag ist.

Wir betrachten Dithering nur für eine Darstellung als Schwarz/Weiß-Bild.

Dithermatrizen sind üblicherweise quadratisch und enthalten ganzzahlige Einträge von $0$ bis $n^2-1$, wobei $n$ die Matrixgröße angibt.

Mögliche Dithermatrizen sind:

$$D^{(2)} = \left(\begin{array}{cc}3&1\\ 0&2\end{array}\right) ... ...&0&1&18\\ 12&8&3&7&13\\ 24&18&19&11&22 \end{array}\right)$$

$$D^{(3)} = \left(\begin{array}{ccc}2&6&4\\ 5&0&1\\ 8&3&7\end{a... ...&8&2&10\\ 12&4&14&6\\ 3&11&1&9\\ 15&7&13&5 \end{array}\right)$$

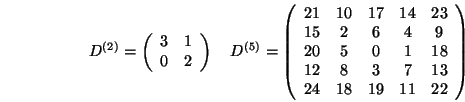
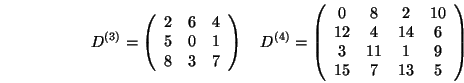
Dithermatrizen höherer Ordnung kann man mithilfe folgender Rekursion berechnen:

$$D^{(2n)} = \left(\begin{array}{cc} 4D^{(n)}+3U^{(n)} & 4D^{(n)}+U^{(n)}\\ 4D^{(n)} & 4D^{(n)}+2U^{(n)} \end{array}\right)$$

mit $U^{(n)}$ sind vollbesetzte Matrizen mit 1-Einträgen.

Die Intensität des Originalbildes wird in das Intervall $[0,n^2]$ skaliert und ein Pixel wird gesetzt, wenn:

$$I(x,y)>D(x\,\mbox{mod}\,n,y\,\mbox{mod}\,n)$$

Eigenschaften:

• Auflösung bleibt erhalten
• die Größe der Dithermatrix bestimmt die Anzahl der darstellbaren Graustufen
• in der Praxis werden Dithermatrizen bis Größe 10 verwendet, d.h. nur Pixel mit Intensität oberhalb eines Schwellwertes werden gesetzt.
• man kann auch eine Dithermatrix mit nur einem Eintrag $0$ verwenden
• Dithering ist parallelisierbar