



Nächste Seite: Kanonische Sichtvolumen
Aufwärts: 3-dimensionale Darstellung
Vorherige Seite: Weltkoordinaten in Kamerakoordinaten
Inhalt
Unterabschnitte
Es gibt verschiedene Möglichkeiten die Projektion der
3-dimensionalen Objekte auf/in eine 2-dimensionale Projektionsfläche
vorzunehmen. Beispiele sind:
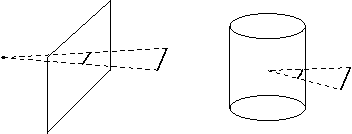
- geradlinige Projektion auf eine Ebene
- geradlinige Projektion auf einen Zylindermantel
- krummlinige Projektionen (z.B. um Linseneffekte zu erzeugen)
Wir betrachten hier nur die Projektion auf eine Ebene.
Hier werden zueinander parallele Geraden verwendet, um Punkte
aus dem Objektraum auf die Bildebene zu projizieren.
Hierbei bleiben parallele Linien im Objektraum als parallele Linien
in der Projektion erhalten.
Man unterscheidet:
- rechtwinklige Projektion:
Die Projektionsmatrix der rechtwinkligen Projektion
ergibt sich recht einfach als:
d.h. man kann einfach zur Berechnung der Projektion eines Punktes
dessen  -Koordinate weglassen.
-Koordinate weglassen.
Man unterscheidet weiter (insbesondere für CAD Zwecke):
- Hauptrisse
Man wählt den Normalenvektor der Kamera parallel
zu einer Koordinatenachse des Weltkoordinatensystems und
erhält so Seitenansichten.
- axonometrische Risse
Man wählt den Normalenvektor der Kamera so, dass
die Projektionsebene mehrere Koordinatenachsen des
Weltkoordinatensystems schneidet:
- dimetrische Projektion:
- zwei Achsen werden geschnitten
- trimetrische Projektion:
- alle Achsen werden geschnitten
- isometrische Projektion:
- alle Achsen werden geschnitten, und zwar so, dass die
entstehenden Achsenabschnitte gleiche Länge haben;
damit bleiben in der Projektion die originalen
Längenverhältnisse erhalten.
- schiefwinklige Projektion:
Damit können wir folgende Berechnungen durchführen:
Der projizierte Punkt
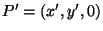 berechnet sich mit den angegebenen Winkeln und Längen wie folgt:
berechnet sich mit den angegebenen Winkeln und Längen wie folgt:
wobei
und die Projektionsmatrix ergibt sich zu:
was mit  gerade die rechtwinklige Projektionsmatrix darstellt.
gerade die rechtwinklige Projektionsmatrix darstellt.
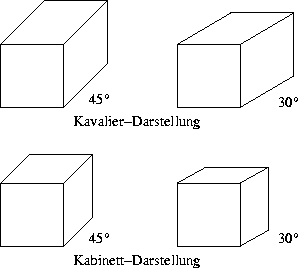
Man unterscheidet entsprechend der Winkel im CAD Bereich:
- Kavalier-Darstellung:
- Die senkrecht zur Projektionsebene verlaufenden Objektkanten
werden unverkürzt dargestellt, d.h.
und übliche Wahlen von  sind:
sind:
- Kabinett-Darstellung:
- Die senkrecht zur Projektionsebene verlaufenden Objektkanten
werden um den Faktor 2 verkürzt dargestellt, d.h.
und übliche Wahlen von  sind ebenfalls:
sind ebenfalls:
Will man ein interaktives System implementieren, in dem der Benutzer
 und
und  bzw.
bzw. 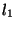 angibt, so sollte man darauf achten,
dass u.U.
angibt, so sollte man darauf achten,
dass u.U. 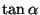 nicht berechnet werden kann.
nicht berechnet werden kann.
Hier werden Geraden verwendet, die in einem Fokuspunkt zusammenlaufen,
um einen Punkt aus dem Objektraum auf die Bildebene zu projizieren.




Nächste Seite: Kanonische Sichtvolumen
Aufwärts: 3-dimensionale Darstellung
Vorherige Seite: Weltkoordinaten in Kamerakoordinaten
Inhalt
© 2004/2005, A. Formella & D. Fellner, Universität Braunschweig
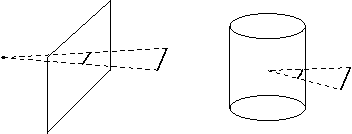
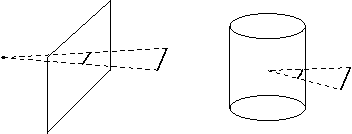
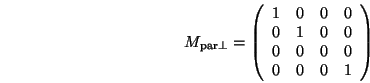
![]() -Koordinate weglassen.
-Koordinate weglassen.
![]() berechnet sich mit den angegebenen Winkeln und Längen wie folgt:
berechnet sich mit den angegebenen Winkeln und Längen wie folgt:

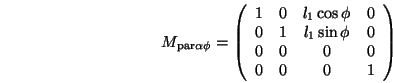

![]() und
und ![]() bzw.
bzw. ![]() angibt, so sollte man darauf achten,
dass u.U.
angibt, so sollte man darauf achten,
dass u.U. ![]() nicht berechnet werden kann.
nicht berechnet werden kann.