Weltkoordinaten in Kamerakoordinaten

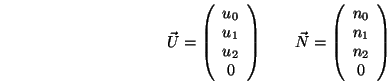
Die Umrechnung von Modellkoordinaten in Weltkoordinaten erfolgt durch entsprechende Transformationen, wie wir sie in vorigen Abschnitten beschrieben haben.

Die Umrechnung von Weltkoordinaten in Kamerakoordinaten ist wegen der orthonormalen Basen auch recht einfach:

$${\vec U}= \left(\begin{array}{c}u_0\\ u_1\\ u_2\\ 0\end{array... ...}= \left(\begin{array}{c}n_0\\ n_1\\ n_2\\ 0\end{array}\right)$$

$${\vec V}= \left(\begin{array}{c}v_0\\ v_1\\ v_2\\ 0\end{array... ...}= \left(\begin{array}{c}c_0\\ c_1\\ c_2\\ 1\end{array}\right)$$

und damit Translationsmatrix

$$T_c=\left(\begin{array}{cccc} 1 & 0 & 0 & -c_0 \\ 0 & 1 & ... ...1 \\ 0 & 0 & 1 & -c_2 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

und Rotationsmatrix

$$R_{uvn}=\left(\begin{array}{cccc} u_0 & u_1 & u_2 & 0 \\ v... ...\ n_0 & n_1 & n_2 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

und somit ist die Transformationsmatrix für Weltkoordinaten in Kamerakoordinaten

$$M_{\mathrm{cam}}=R_{uvn} \cdot T_c$$

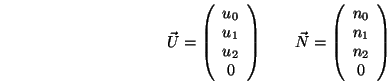
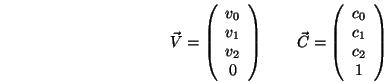
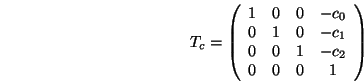
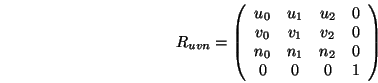
Man sieht leicht ein, dass diese Matrizen korrekt sind, denn die Kamerabasisvektoren werden auf die kartesischen Basisvektoren und die Kameraposition auf den Ursprung abgebildet:

$$\begin{eqnarray*} R_{uvn}\cdot{\vec U}&=& {\vec e}_0 \\ R_{uvn}\cdot{\vec V}&=&... ...uvn}\cdot{\vec N}&=& {\vec e}_2 \\ T_c\cdot{\vec C}&=& {\vec 0} \end{eqnarray*}$$

Generell gilt: es genügt, vier nicht koplanare Punkte affinepointaufeinander abzubilden, um eine affine Abbildung zu konstruieren (und umgekehrt).