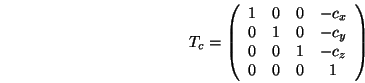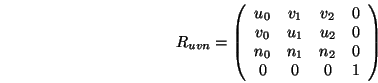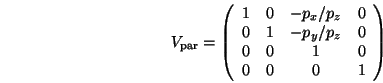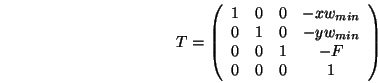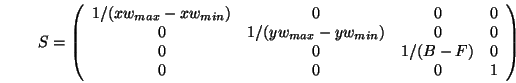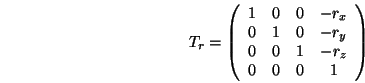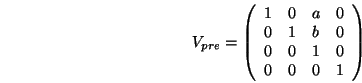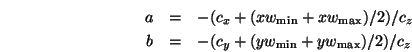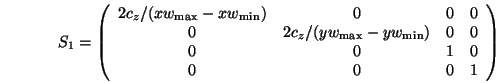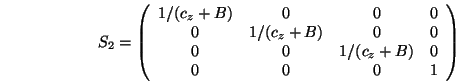Kanonische Sichtvolumen

Für eine Implementierung der Projektion und der Clipping-Operationen (auch bei obiger Parallelprojektion) ist es zweckmäßig, den sichtbaren Bereich der Szene als ein kanonisches Sichtvolumen zu repräsentieren, d.h.

• der Kamerapunkt (bzw. die Kamerarichtung bei der Parallelprojektion) bestimmt mit den Rändern des Ausschnitts der Bildebene, der auf dem Ausgabegerät dargestellt werden soll, die seitlichen Begrenzungsebenen des Sichtvolumens;
• man spezifiziert weiterhin eine vordere und eine hintere Begrenzungsebene (z.B. durch Angabe zweier Distanzen $F$ und $B$ front und back, oder near und far), um das Sichtvolumen vollständig abzuschließen; hierzu verwendet man entweder
  • die durch die Szene vorgegebenen, maximalen Koordinaten bezüglich des Abstandes von der Bildebene,
  • oder die durch den Benutzer angegebenen, maximalen Koordinaten des Teils der Szene, welcher sichtbar sein soll (so will man z.B. häufig, dass die Objekte zwischen Kamerapunkt und Bildebene nicht auf die Bildebene projiziert werden).
• das endliche Sichtvolumen wird durch eine lineare Transformation in ein kanonisches Sichtvolumen (z.B. Einheitswürfel, oder Einheitspyramide mit Grundfläche 2 auf 2 und Höhe 1) transformiert, so dass anschließende Clipping- und Sichtbarkeitsberechnungen einfacher zu berechnen sind.

Parallelprojektion

Berechnung eines kanonischen Sichtvolumens für die Parallelprojektion

$$K_{\mathrm{par}}=S\cdot T\cdot V_{\mathrm{par}}\cdot R_{uvn}\cdot T_c$$

wobei

$$T_c = \left(\begin{array}{cccc} 1 & 0 & 0 & -c_x \\ 0 & 1 & ... ...-c_y \\ 0 & 0 & 1 & -c_z \\ 0 & 0 & 0 & 1 \end{array}\right)$$

den Ursprung in den Kamerapunkt verschiebt,

$$R_{uvn} = \left(\begin{array}{cccc} u_0 & v_1 & v_2 & 0 \\ v... ...0 \\ n_0 & n_1 & n_2 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

die Weltkoordinaten in Kamerakoordinaten transformiert,

$$V_{\mathrm{par}} = \left(\begin{array}{cccc} 1 & 0 & -p_x/p_z... ...p_z & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

durch eine Scherung die schiefwinklige Projektion in eine orthogonale umwandelt,

$$T= \left(\begin{array}{cccc} 1 & 0 & 0 & -xw_{min} \\ 0 & 1 ... ..._{min} \\ 0 & 0 & 1 & -F \\ 0 & 0 & 0 & 1 \end{array}\right)$$

den Ursprung in eine Ecke des Quaders verschiebt,

$$S= \left(\begin{array}{cccc} 1/(xw_{max}-xw_{min}) & 0 & 0 & ... ...0 \\ 0 & 0 & 1/(B-F) & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

den Quader zum Einheitswürfel skaliert.

Zentralprojektion

Berechnung eines kanonischen Sichtvolumens für die Zentralprojektion

Betrachten wir folgenden etwas vereinfachten Fall, d.h. der Fokuspunkt der Projektion liegt auf der $n$-Achse des Kamerakoordinatensystems:

$$K_{per}=S_2\cdot S_1\cdot V_{pre}\cdot T_r\cdot R_{uvn}\cdot T_c$$

wobei

$$T_r = \left(\begin{array}{cccc} 1 & 0 & 0 & -r_x \\ 0 & 1 & ... ...-r_y \\ 0 & 0 & 1 & -r_z \\ 0 & 0 & 0 & 1 \end{array}\right)$$

den Ursprung in den Fokuspunkt verschiebt (stimmt die Kameraposition mit dem Fokuspunkt überein, was wohl der in der Praxis verwendete Fall ist, dann braucht nicht verschoben zu werden, d.h. 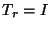$T_r=I$)

$$V_{pre} = \left(\begin{array}{cccc} 1 & 0 & a & 0 \\ 0 & 1 & b & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

mit

$$\begin{eqnarray*} a&=&-(c_x+(xw_{\mathrm{min}}+xw_{\mathrm{max}})/2)/c_z \\ b&=&-(c_y+(yw_{\mathrm{min}}+yw_{\mathrm{max}})/2)/c_z \end{eqnarray*}$$

durch eine Scherung die Mittellinie des Sichtvolumens in die $z$-Achse ($n$-Achse) transformiert,

$$S_1= \left(\begin{array}{cccc} 2c_z/(xw_{\mathrm{max}}-xw_{\m... ...& 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

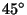durch eine $xy$-Skalierung die seitlichen Begrenzungsebenen zu $45^\circ$-Ebenen neigt,

$$S_2= \left(\begin{array}{cccc} 1/(c_z+B) & 0 & 0 & 0 \\ 0 & ... ...\\ 0 & 0 & 1/(c_z+B) & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

die Pyramide zur Einheitspyramide skaliert.

Diese Pyramide kann auch in den Einheitswürfel transformiert werden.

Tun Sie dies!