Quadriken

Kugel

Für einen Punkt der Oberfläche gilt (implizite Gleichung):

$$\begin{eqnarray*} \vert{\vec x}-{\vec c}\vert &=& r \\ \langle{\vec x}-{\vec c},{\vec x}-{\vec c}\rangle &=& r^2 \end{eqnarray*}$$

Für ${\vec c}={\vec 0}$ erhält man

$$x^2+y^2+z^2=r^2$$

oder in parametrisierter Form für $\phi\in[0,2\pi[$ und $\delta\in[-\pi/2,\pi/2]$

$$\begin{eqnarray*} x &=& r\cdot\cos\delta\,\cos\phi \\ y &=& r\cdot\sin\delta \\ z &=& r\cdot\cos\delta\,\sin\phi \end{eqnarray*}$$

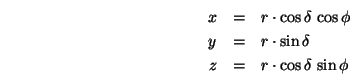
Beachte bzgl. welcher Achse die Winkel definiert werden (z.B. kann man auch Standardpolarkoordinaten verwenden), hier hat man verschiedene Freiheitsgrade. Oft bildet man die Winkel in das $(u,v)$-Einheitsquadrat ab, d.h. läuft $u$ von 0 nach 1, so läuft $\phi$ von 0 bis $2\pi$. Welche Substitution führt man konkret durch?

Darstellung einer Kugel z.B. durch Umwandlung der Kugel in ein Polyeder.

Klassische Methode durch Diskretisierung von Azimuth und Elevation (hier nur die sichtbaren Kanten dargestellt):

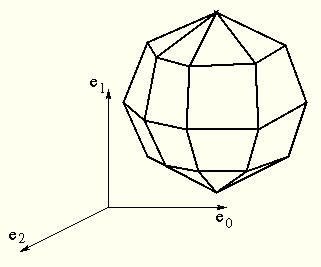
Andere Methode durch sukkzessive Unterteilung eines regulären Grundkörpers.

z.B. Grundkörper Tetraeder

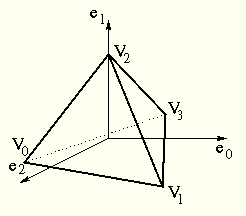
jede Kante wird in der Mitte geteilt und die entstehende Ecke auf die Kugeloberfläche projiziert:

Am Beispiel eines Dreiecks des Tetraeders:

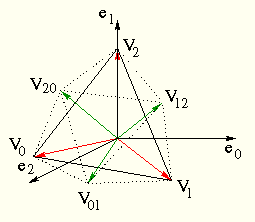
oder in der Darstellung als planarer Graph für eine Unterteilung der ersten Stufe:

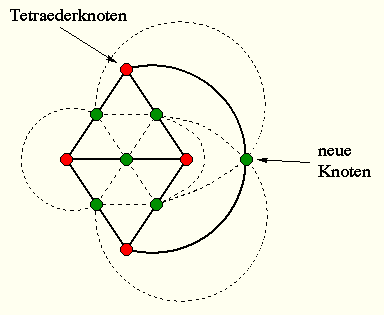
Die Knoten des planaren Graphen haben alle Grad 6 mit der Ausnahme der ursprünglichen Tetraeder-Knoten, die nur Grad 3 haben.

Es ergibt sich durch Fortsetzen der Unterteilung der Dreiecke ein Baum mit Grad 5 (d.h. 4 Kinder je innerem Knoten):

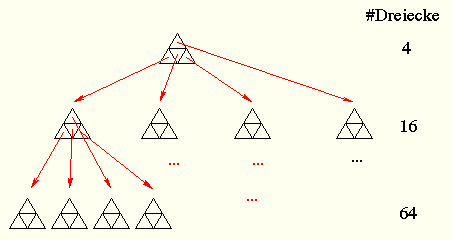
Und man kann je nach gewünschter Feinheit der Unterteilung entsprechend alle Dreiecke in einer bestimmten Stufe des Baumes zur Darstellung heranziehen.

Statt des Tetraeders kann ein anderer platonischer Körper als Grundkörper herangezogen werden:

Körper	#Ecken	Fassettenform
Tetraeder	4	Dreiecke
Würfel	8	Vierecke
Oktaeder	6	Dreiecke
Dodekaeder	20	Fünfecke
Ikosaeder	12	Dreiecke

Vorzugsweise nimmt man einen Grundkörper mit Dreiecken als Fassettenform, ansonsten muss man vorher entsprechend in Dreiecke zerlegen.

Beim Oktaeder steigt der Grad der ersten Knoten im planaren Graphen auf 4, beim Ikosaeder sogar auf 5, alle weiteren sukkzessive konstruierten Knoten (Ecken) haben dann Grad 6.

Ellipsoid

Implizite Gleichung eines Ellipsoiden:

$$\left(\frac{x}{r_x}\right)^2+ \left(\frac{y}{r_y}\right)^2+ \left(\frac{z}{r_z}\right)^2=1$$

oder mit Skalierungsmatrix $M_s$

$$\langle M_s{\vec X},M_s{\vec X}\rangle =r^2$$

wobei die Skalierungsmatrix folgende Form hat

$$M_s = \left(\begin{array}{ccc}r/r_x & 0 & 0\\ 0 & r/r_y & 0\\ 0 & 0 & r/r_z\end{array}\right)$$

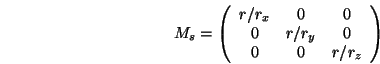
Parametrische Gleichung eines Ellipsoiden:

$${\vec X}=\left(\begin{array}{c}r_x\;\cos\delta\;\cos\phi\\ r_y\;\sin\delta\\ r_z\;\cos\delta\sin\phi\end{array}\right)$$

mit $\phi\in[0,2\pi[$ und $\delta\in[-\pi/2,\pi/2]$.

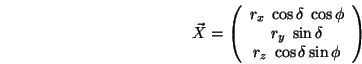
Ein Ellipsoid ist also nichts anderes als eine skalierte Kugel.

Torus

Implizite Gleichung eines Torus:

$$\left(r-\sqrt{ \left(\frac{x}{r_x}\right)^2+ \left(\frac{y}{r_y}\right)^2}\right)^2+ \left(\frac{z}{r_z}\right)^2=1$$

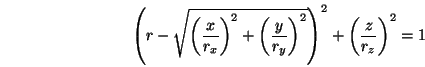
Parametrische Gleichung eines Torus:

$${\vec X}=\left(\begin{array}{c}r_x(r+\cos\delta)\cos\phi\\ r_y\;\sin\delta\\ r_z(r+\cos\delta)\sin\phi\end{array}\right)$$

mit $\phi,\delta\in[-\pi,\pi]$.

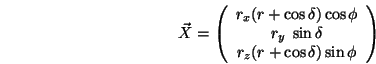
Es gibt noch mehr Quadriken (z.B. Paraboloid, Hyperboloid usw.) deren Beschreibungen ähnlich erfolgen, auf die an dieser Stelle jedoch nicht näher eingegangen wird.