Superquadriken

Superquadriken stellen eine Verallgemeinerung der Quadriken dar. Mithilfe der Einführung weiterer besonders gewählter Parameter lässt sich die ursprüngliche Form der Quadrik modifizieren.

Auch hier betrachten wir nur eine Auswahl der Quadriken.

2-dimensionale Superquadriken

Superellipse

Implizite Gleichung einer Ellipse:

$$\left(\frac{x}{r_x}\right)^2+ \left(\frac{y}{r_y}\right)^2=1$$

wir führen einen Parameter $s\not=0$ wie folgt ein:

$$\left(\frac{x}{r_x}\right)^{\frac{2}{s}}+ \left(\frac{y}{r_y}\right)^{\frac{2}{s}}=1$$

oder auch in der parametrischen Gleichung:

$$\begin{eqnarray*} x&=&r_x\;\cos^s\phi \\ y&=&r_y\;\sin^s\phi \end{eqnarray*}$$

mit $\phi\in[0,2\pi[$, was man durch Einsetzen leicht verifiziert:

$$\begin{eqnarray*} \left(\frac{r_x\;\cos^s\phi}{r_x}\right)^{\frac{2}{s}}+ \lef... ...hi}{r_y}\right)^{\frac{2}{s}}&=&1 \\ \cos^2\phi+\sin^2\phi&=&1 \end{eqnarray*}$$

3-dimensionale Superquadriken

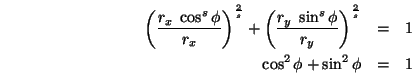
Analog wie im 2-Dimensionalen führen wir--um ein Superellipsoid zu erhalten--zwei Parameter ein.

Implizite Gleichung eines Ellipsoiden:

$$\left(\frac{x}{r_x}\right)^2+ \left(\frac{z}{r_z}\right)^2+ \left(\frac{y}{r_y}\right)^2=1$$

wir führen zwei Parameter $s_1,s_2\not=0$ wie folgt ein:

$$\left(\left(\frac{x}{r_x}\right)^{\frac{2}{s_1}}+ \left(\fra... ...frac{s_1}{s_2}}+ \left(\frac{y}{r_y}\right)^{\frac{2}{s_2}}=1$$

oder auch in der parametrischen Gleichung:

$$\begin{eqnarray*} x&=&r_x\;\cos^{s_1}\delta\;\cos^{s_2}\phi \\ z&=&r_z\;\cos^{s_1}\delta\;\sin^{s_2}\phi \\ y&=&r_y\;\sin^{s_2}\delta \end{eqnarray*}$$

was man auch durch Einsetzen leicht verifiziert.

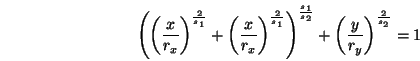
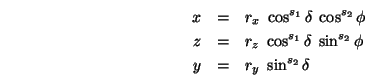
Wie sehen solche Superquadriken aus?