Polygonale Objekte

Als polygonale Objekte oder Polyeder bezeichnen wir Objekte, deren Oberfläche durch Polygone beschrieben wird (polygon meshes).

Beispiel:

Repräsentation eines solchen Objektes:

• Punktliste (oder Eckenliste)
  
  $$V_0, V_1, V_2, V_3, V_4, V_5$$
  
  

• und Kantenliste
  
  $$E_0=(V_0,V_1); E_1=(V_1,V_3); E_2=(V_3,V_5); \dots$$
  
  

• und Polygonliste
  • als Punktlisten
    
    $$S_0=(V_0,V_1,V_3,V_5); S_1=(V_1,V_2,V_3); \dots$$
    
    

  • oder Kantenlisten
    
    $$S_0=(E_0,E_1,E_2,E_4); \dots$$
    
    

Ob die Polygonliste gebraucht wird, hängt von der Anwendung ab (für Drahtgittermodelle z.B. wird sie nicht benötigt). Außer der Punktliste enthalten die Datenstrukturen nur Zeiger oder Indizes.

Häufig sind meshes nur dreiecks- und/oder vierecksbasiert.

Oberfläche als Graph

In manchen Anwendungen ist es sinnvoll, einen gesamten Graphen (als Datenstruktur) der Oberfläche abzuspeichern.

Oberfläche ist Graph, Ecken sind Knoten, Kanten sind Kanten.

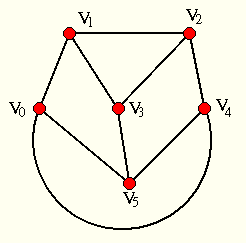
Ist das Objekt nicht entartet, so ist der Graph ist planar.

Ordne die Kanten an einem Knoten:

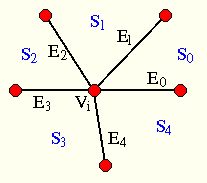
Damit lassen sich durch Angabe jeweils einer Kante leicht die Polygone der Fassetten des Polyeders angeben:

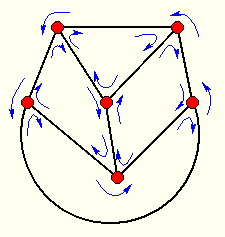
Das heißt für ein Polygon einer Fassette genügt ein Zeiger auf eine Kante im Graphen.

Hierbei sollten weitere Anforderungen an einen planaren Graphen gestellt werden, um keine entarteten Polyeder zu erhalten. Hierauf soll jedoch nicht weiter eingegangen werden.

Innen und Außen:

Oberfläche ist Menge von Polygonen (deren Ecken und Kanten durch Suche in einem planaren Graphen gefunden werden kann).

Was ist Innen bzw. Außen?

Normalerweise gehen wir davon aus, dass wir als Betrachter außen stehen.

Ebenengleichung einer Fassette:

Nehmen wir an, wir hätten den Normalenvektor ${\vec N}$ für eine Fassette schon gegeben. Für jeden Punkt ${\vec P}$ der Ebene der Fassette gilt dann:

$$\begin{eqnarray*} \langle{\vec P}-{\vec V}_0,{\vec N}\rangle &=&0 \end{eqnarray*}$$

Dies können wir anders schreiben und ${\vec P}=(x y z)^\top$ sowie ${\vec N}=(A B C)^\top$ einsetzen

$$\begin{eqnarray*} \langle{\vec P},{\vec N}\rangle \underbrace{-\langle{\vec V}_0,{\vec N}\rangle }_{\displaystyle =D}&=&0\\ Ax+By+Cz+D&=&0 \end{eqnarray*}$$

und erhalten die übliche Schreibweise einer impliziten Ebenengleichung.

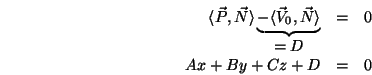
Mit dieser impliziten Ebenengleichung definieren wir oberhalb und unterhalb bezüglich dieser Fassette analog wie wir es bereits beim Polygon gesehen haben:

$$\begin{eqnarray*} \langle{\vec P},{\vec N}\rangle +D &=& \left\{\begin{array}{l... ...ache} \\ > & 0 & \quad\mbox{innerhalb} \\ \end{array}\right. \end{eqnarray*}$$

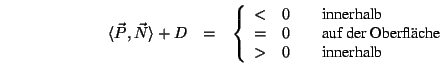
Ebenso analog wie beim Polygon definieren wir:

• Ein Punkt liegt außerhalb eines konvexen Polyeders, wenn er bezüglich aller seiner Fassetten oberhalb liegt.
• Ein Punkt liegt außerhalb des Polyeders, wenn die Anzahl der von einem Strahl geschnittenen Fassetten gerade ist, sonst innerhalb (`odd-even Methode').

Im normalen Sprachgebrauch ist die Konvention, dass ein Normalenvektor einer Fassette nach oben bzw. nach außen zeigt.