3-Dimensionale Polygone

3-Dimensionale Polygone können genau wie 2-dimensionale Polygone durch eine zyklische Liste von Punkten $p_0,\dots,p_{n-1}$ beschrieben werden.

Normalenvektorberechnung von fast planaren Polygonen

Eine naive Methode für eine Normalenvektorberechnung basiert auf dem Vektorkreuzprodukt:

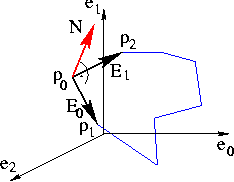
Nehmen 2 nicht linear abhängige Kantenvektoren und bilden einen Normalenvektor der Ebene der Fassette:

$$\begin{eqnarray*} {\vec E}_0&=&{\vec V}_1-{\vec V}_0\\ {\vec E}_1&=&{\vec V}_2-{\vec V}_0\\ N &=& E_0\times E_1 \end{eqnarray*}$$

Jedoch

• die Ecken eines im 3-Dimensionalen gegebenen Polygons liegen u.U. nicht genau in einer Ebene
  • Rechenungenauigkeiten
  • ungenaue Eingabewerte
• obige Rechnung mit Kreuzprodukt zweier Kantenvektoren setzt voraus, dass die Kantenvektoren nicht linear abhängig sind; diese muss man erst einmal bestimmen.

Deshalb folgende--numerisch stabile--Methode um einen Normalenvektor zu bestimmen:

Berechnen die Flächen der Projektionen des Polygons in die drei Koordinatenebenen:

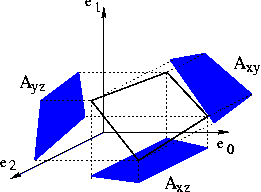
Ein Normalenvektor ergibt sich dann als

$$\begin{eqnarray*} {\vec N}&=&\left(\begin{array}{c}A_{yz}\\ -A_{xz}\\ A_{xy}\end{array}\right) \end{eqnarray*}$$

Das sieht man wie folgt ein:

$$\begin{eqnarray*} A_{yz}&=& A\cdot\cos\alpha \\ &=& A\cdot\langle{\vec N},{\vec e}_0\rangle /\vert{\vec N}\vert \\ &=& A\cdot N_x \end{eqnarray*}$$

also

$$\begin{eqnarray*} N_x&=&A_{yz}/A \end{eqnarray*}$$

und analog

$$\begin{eqnarray*} N_y&=&-A_{xz}/A\\ N_z&=&A_{xy}/A \end{eqnarray*}$$

und der normierte Normalenvektor ist:

$$\begin{eqnarray*} {\mathbf N}&=&\frac1A\cdot\left(\begin{array}{c}A_{yz}\\ -A_{xz}\\ A_{xy}\end{array}\right) \end{eqnarray*}$$

insbesondere ergibt sich auch:

$$\begin{eqnarray*} A&=&\sqrt{A_{xy}^2+A_{xz}^2+A_{yz}^2} \end{eqnarray*}$$

Planaritäts- und Einfachheit/Konvexitätstest

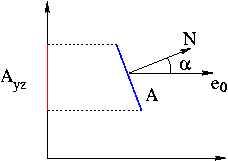
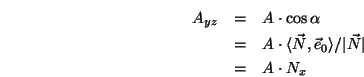
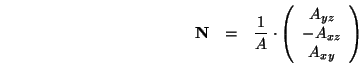
Um zu überprüfen, ob das Polygon hinreichend planar ist, berechnet man z.B. den Abstand der einzelnen Punkte zu der Ebene, welche durch den Normalenvektor und das Zentrum

$$c= \frac 1n\sum_{i=0}^{n-1} p_i$$

gegeben ist.

Für die Abstände ergibt sich dann:

$$d_i = \langle N,p_i-c\rangle = \langle N,p_i\rangle - \langle N,c\rangle$$

Sind alle Abstände hinreichend klein oder hat man die Punkte entlang des Normalenvektors hinreichend nahe an die Ebene geschoben, so kann das Polygon als planar angesehen werden.

Um zu überprüfen, ob das Polygon einfach und konvex ist, arbeitet man zweckmäßigerweise in der dominaten Ebene, d.h. man projiziert das 3D Polygon in die Koordinatenebene auf der die größte Normalenvektorkomponente senkrecht steht. Der Test auf Einfachheit und Konvexität erfolgt dann in Linearzeit in Anzahl der Ecken durch 2D Berechnungen.