Condiciones para un análisis multiresolución

fijamos las condiciones que nos llevan a un análisis multiresolución en un marco independiente de los ejemplos concretos

tenemos un análisis multiresolución ortonormal basado en una función de escalado $\varphi$ con

$$\varphi_i^j(x)=\sqrt{2^j}\varphi(2^jx-i)$$

y una secuencia de números $c_k$ ($k\in\bbbz$) cuando se cumplen las siguientes propriedades

1. ortonormalidad

   
   

   $$\langle\varphi_i^0,\varphi\rangle =\delta_{i0} \qquad i\in\bbbz$$
   
   

2. relación de dos escalas

   
   

   $$\varphi=\sum_{k\in\bbbz}c_k\varphi_k^1$$
   
   

3. propriedad de promediar

   
   

   $$\int_\bbbr \varphi(x)dx=1$$
   
   

comentamos las propriedades

1. • porque el producto escalar está basado en integrales y porque trabajamos sobre intervalos de potencias de dos, basta con exigir la ortonormalidad respeto a la función de escalado padre
   • la condición de la ortonormalidad se puede aflojar como veremos después
2. • vemos que se representa una función de base del $V^0$ con funciones de base del $V^1$
   • la condición se puede escribir igual como

     
     

     $$\varphi(x)=\sqrt{2}\sum_{k\in\bbbz}c_k\varphi(2x-k)$$
     
     

   • la condición se traslada directamente a todas las escalas
     $$\begin{eqnarray*} \varphi_i^j&=&\sum_{k\in\bbbz}c_k\varphi_{k+2i}^{j+1} \\ &=&\sum_{k\in\bbbz}c_{k-2i}\varphi_{k}^{j+1}\\ &\in&V^{j+1} \end{eqnarray*}$$
     
     
     
     
     

   • la condición indica nada más que se genera la cadena de inclusiones, es decir, $\varphi$ está contenido en $V^0$ y si se puede representar una función en $V^j$ (con las funciones $\varphi_i^j$ siendo una base en este espacio) también se puede representar la función en $V^{j+1}$
   • los coeficientes $c_k$ se llaman también coeficientes de filtrado
3. formalmente se debe argumentar con bases de Riesz y propriedades de convergencias que no incluimos aquí

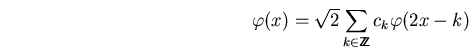
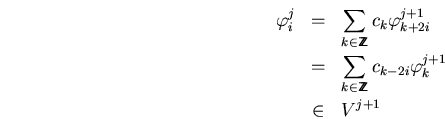
como consecuencia obtenemos las siguientes características importantes de los coeficientes de filtrado

$$\begin{eqnarray*} \sum_{k\in\bbbz}c_k&=&\sqrt{2} \\ \sum_{k\in\bbbz}c_kc_{k-2i}&=&\delta_{i0} \qquad \forall i \end{eqnarray*}$$

que se verifica fácilmente:

•  
  
  $$\begin{eqnarray*} \varphi(x) &=& \sqrt{2}\sum_{k\in\bbbz}c_k\varphi(2x-k) \ ... ...varphi(t)}{2}dt \\ &=& \frac{1}{\sqrt{2}}\sum_{k\in\bbbz}c_k \end{eqnarray*}$$
  
  
  
  
  

•  
  
  $$\begin{eqnarray*} \delta_{i0} &=& \langle\varphi_i^0,\varphi\rangle \\ &=& ... ...bbz}c_k\varphi_k^1\rangle \\ &=& \sum_{k\in\bbbz}c_kc_{k-2i} \end{eqnarray*}$$
  
  
  
  
  

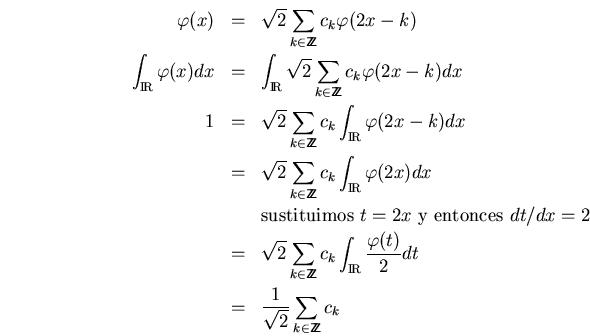
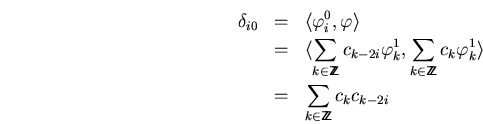
hasta ahora vimos solamente las funciones de escalado de Haar, otro ejemplo serán las funciones de escalado de Shannon dados por

$$\begin{eqnarray*} \varphi &=& \frac{\sin(\pi t)}{\pi t} \\ \end{eqnarray*}$$

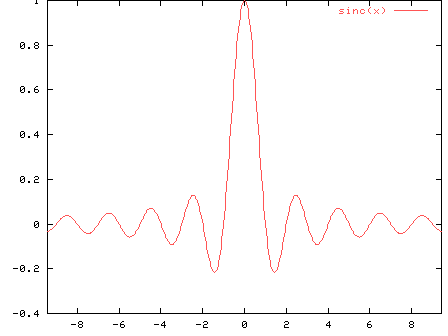
la comprobación de las propriedades necesarias para que sea un análisis multiresolución se hace mejor usando la transformada de Fourier y sus propriedades, lo dejamos en este momento ...

solo cabe decir, que las funciones de escalado de Shannon se comportan en el espacio de las frecuencias como las funciones de escalado de Haar en el espacio de tiempo, en el sentido, que la transformada de Fourier de la función de Shannon resulta en una función de caja, es decir, parecido a la función de escalado de Haar, y al revés, la transformada de Fourier de la función de escalado de Haar es parecido a la función de Shannon

así ambos sistemas representan los dos extremos en el espacio de tiempo y de las frecuencias