dado un análisis multiresolución ortonormal, queremos construir
una base del espacio
![]()
los propios ![]() no generan una base ortonormal por dos razones:
no generan una base ortonormal por dos razones:
sabemos
entonces, intentamos ampliar el conjunto de ![]() para obtener
una base del
para obtener
una base del ![]()
empezamos con el ![]() , es decir, tenemos como base los
, es decir, tenemos como base los ![]() (
(![]() )
)
dentro de ![]() tenemos los
tenemos los

queremos que las ![]() , siendo las funciones nuevas, también se generan
con traslación y dilatación simple
, siendo las funciones nuevas, también se generan
con traslación y dilatación simple
hacemos el ansatz

y queremos que los coeficientes ![]() sean de tal manera que el sistema
de los
sean de tal manera que el sistema
de los ![]() más los
más los ![]() formen una base ortonormal
del
formen una base ortonormal
del ![]()
Cómo lo haríamos en el ![]() ?
?
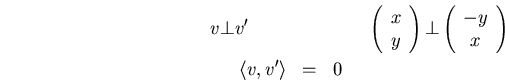
o generalmente en un espacio de dimensión ![]()
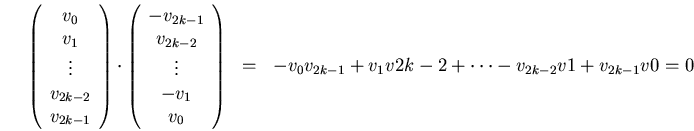
mostramos el cálculo de los ![]() en un caso especial de los
espacios de funciones para captar la idea:
en un caso especial de los
espacios de funciones para captar la idea:
asumimos que tengamos solamente 6 ![]() diferentes a zero, es decir,
diferentes a zero, es decir,

o en otra notación
definimos los ![]() entonces, por ejemplo, como
entonces, por ejemplo, como
entonces

escribimos los productos escalares de todos los ![]() y
y ![]() para comprobar la ortonormalidad
para comprobar la ortonormalidad
para los ![]() tenemos
tenemos
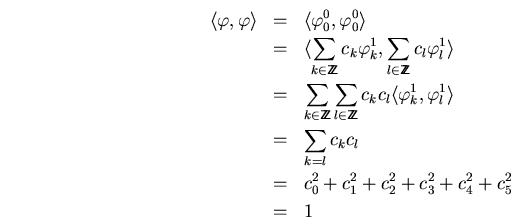
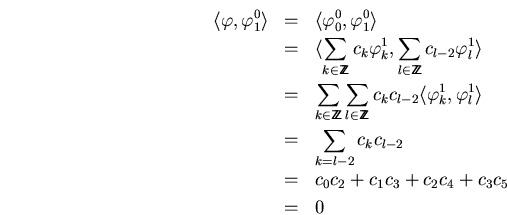

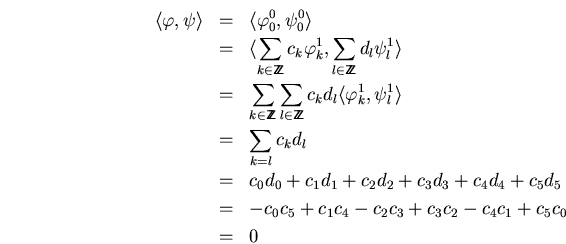
y igual
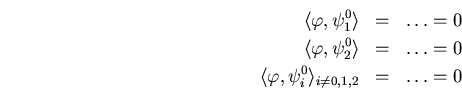
entonces, hemos comprobado que el sistema es ortonormal, y queda la pregunta: es también una base?
(falta algo)