idea de la comprobación que podemos aproximar cualquier función
de
![]()
ya vimos que podemos aproximar una funcion ![]() con la aproximación
con la aproximación
![]() que es una suma de funciones de cajas de anchura
que es una suma de funciones de cajas de anchura ![]()
en los intervalos donde la aproximación es constante la función de escalones tiene el valor
(la media de la integral sobre el intervalo)
podemos realizar una aproximación arbitrariamente fina, si incrementamos
![]()
miramos dos de estas aproximaciones con índice ![]() y
y ![]()
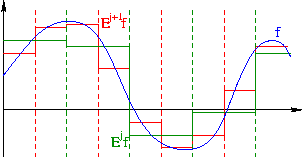
porque los valores de las funciones de escalones ![]() y
y ![]() son las medias de las integrales sobre los intervalos adecuados y
dichos intervalos se cortan por la mitad yiendo de
son las medias de las integrales sobre los intervalos adecuados y
dichos intervalos se cortan por la mitad yiendo de ![]() a
a ![]() tenemos
tenemos

o en otras palabras, porque podemos construir la función ![]() sobre cada intervalo
sobre cada intervalo ![]() de la función
de la función ![]() sumando la ondícula de
Haar
sumando la ondícula de
Haar ![]() multiplicado con un valor
multiplicado con un valor ![]() adecuado,
tenemos la combinación lineal para la diferencia de ambas aproximaciones
adecuado,
tenemos la combinación lineal para la diferencia de ambas aproximaciones
la amplitud de ![]() es
es ![]() , por eso se calculan los
, por eso se calculan los ![]() con
con

iteramos la penúltima ecuación
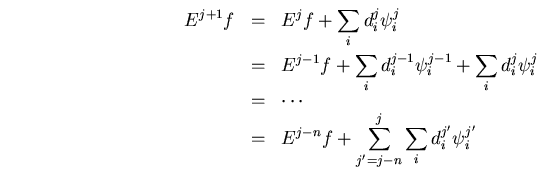
es decir, si empezamos con un
![]() podemos refinar la
aproximación hasta cierto
podemos refinar la
aproximación hasta cierto ![]() , entonces, reescribimos la
fórmula (usando de nuevo
, entonces, reescribimos la
fórmula (usando de nuevo ![]() por
por ![]() )
)
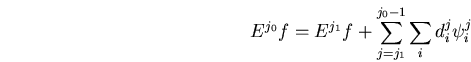
porque
![]() si
si
![]() (recordamos que
(recordamos que
![]() )
podemos conseguir que
)
podemos conseguir que ![]() sea tan pequeño como queremos
(empezando con un
sea tan pequeño como queremos
(empezando con un ![]() suficientemente pequeño), en otras palabras,
tenemos la siguiente aproximación de la función
suficientemente pequeño), en otras palabras,
tenemos la siguiente aproximación de la función ![]()

es decir, si elegimos ![]() lo suficientemente grande (las funciones
de cajas sobre intervalos lo suficientemente pequeños),
podemos aproximar la función
lo suficientemente grande (las funciones
de cajas sobre intervalos lo suficientemente pequeños),
podemos aproximar la función ![]() con una suma de las ondículas de Haar
con una suma de las ondículas de Haar