Ortonormalidad de las ondículas de Haar

idea de la comprobación de su ortonormalidad

ya sabemos que son normalizados $\Vert\psi_i^j\Vert=1$, falta por comprobar

$$\langle\psi_i^j,\psi_k^l\rangle =\int_\bbbr \psi_i^j(x)\psi_k^l(x)dx=0 \qquad \mbox{si}\quad i\not=k, j\not=l$$

si los intervalos de soporte no se solapan, la integral es 0, si los intervalos se solapan, debido que los límites de los soportes son potencias de 2, el solapamiento siempre es de la siguiente manera

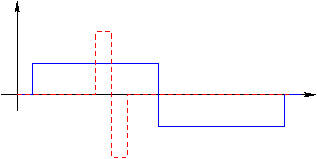
entonces, la integral desvanece (en caso que el solapamiento no es total)