el cálculo de los coeficientes ![]() se basa en los valores
se basa en los valores
![]() que se obtienen calculando integrales sobre intervalos
que se obtienen calculando integrales sobre intervalos
ya vimos en la introducción un algoritmo rápido para calcular la imagen transformada
repetimos el proceso para obtener el algoritmo recursivo
tuvimos las fórmulas
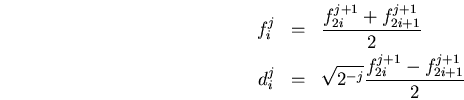
asumimos que tengamos los valores ![]() para un índice
para un índice
![]() suficientemente grande, o en otras palabras,
asumimos que tengamos una aproximación
suficientemente bien de la función
suficientemente grande, o en otras palabras,
asumimos que tengamos una aproximación
suficientemente bien de la función ![]() con una función de escalones
con una función de escalones
incluso podemos aproximar dichos valores ![]() con el valor de
la función
con el valor de
la función ![]() en el centro del intervalo
en el centro del intervalo
entonces podemos calcular todos los ![]() (con
(con ![]() ) y también los
) y también los
![]() recursivamente
recursivamente
desarrollamos las fórmulas
recordamos que pudimos aproximar una función con su proyección
ortogonal usando un sistema de funciones en
![]()

y en el caso especial de usar las funciones de cajas de anchura ![]() y area
y area ![]() tuvimos
tuvimos
pero estas funciones de cajas no son nada más que las funciones de escalado de Haar
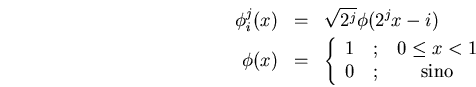
poniendo
![]() adecuadamente, entonces
adecuadamente, entonces

es decir, tenemos para los coeficientes ![]()
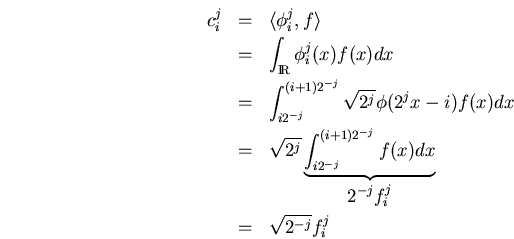
introducimos eso en las ecuaciones del comienzo
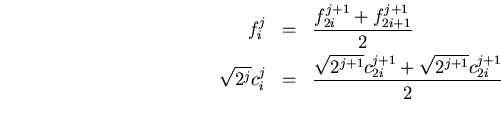
y
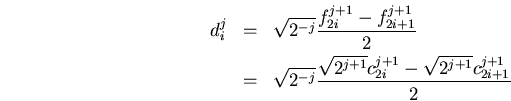
que se reduce a las ecuaciones simétricas y recursivas

siendo la base para el cálculo de la transformación de Haar, o bien, la transformación de ondículas basada en las ondículas de Haar,
si sumamos o sustraemos ![]() y
y ![]() obtenemos las ecuaciones
para el cálculo de la inversa
obtenemos las ecuaciones
para el cálculo de la inversa
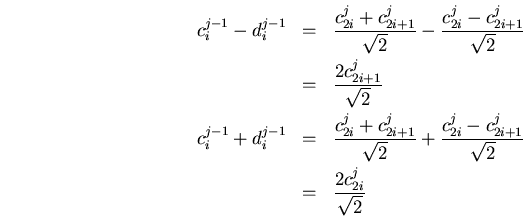
es decir
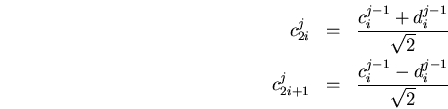
y obtenemos los valores aproximados de la función ![]() como
como