miramos la señal como funciones constantes sobre intervalos
asumimos como dominio el intervalo ![]()
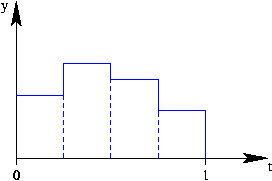
una imagen de un pixel es una función constante sobre el intervalo
![]()
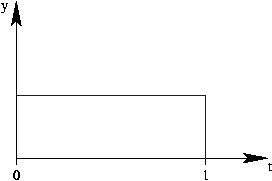
para funciones tenemos la adición y la multiplicación con un
escalar, es decir, podemos tratar las funciones sobre el intervalo
![]() como espacio vectorial de funciones
como espacio vectorial de funciones
(re-estudiamos prevemente los conceptos de espacios vectoriales: vectores, multiplicación escalar, suma, producto escalar, norma, valor absoluto)
llamamos como ![]() el espacio de todas las funciones constantes
sobre
el espacio de todas las funciones constantes
sobre ![]()
igualmente como ![]() el espacio de todas las funciones constantes
sobre los intervalos
el espacio de todas las funciones constantes
sobre los intervalos ![]() y
y ![]()
y sucesivamente ![]() espacio de las funciones constantes sobre
los intervalos equidistantes de anchura
espacio de las funciones constantes sobre
los intervalos equidistantes de anchura ![]()
(sabemos del contexto si ![]() es un superíndice o un exponente)
es un superíndice o un exponente)
con eso: cada imagen (unidimensional) con ![]() pixeles es un
elemento del espacio
pixeles es un
elemento del espacio ![]()
obviamente
![]()
porque
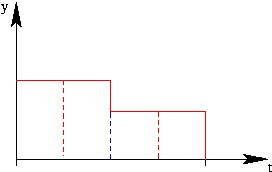
en general
espacios vectoriales tienen bases
conjunto mínimo de vectores del espacio de tal forma que cada vector del espacio se puede expresar como una combinación lineal de los vectores de la base
combinación lineal de ![]()
conjunto mínimo significa que los vectores son linealmente independientes
un espacio vectorial puede tener una dimensión (número de vectores en una base) finita o infinita
llamamos las funciones bases del espacio ![]() funciones de escalado
(anotándolas con
funciones de escalado
(anotándolas con ![]() )
)
observamos que con
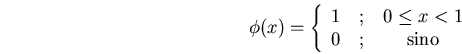
las funciones (funciones de cajas trasladadas)
componen una base del espacio ![]() , p.ej.
, p.ej.
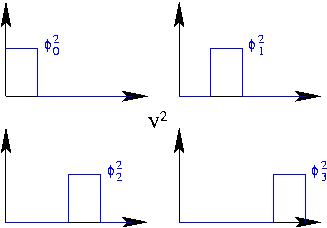
Nota que una función de caja se llama también función característica
![]() donde el intervalo como subíndice indica donde la
función es 1, fuera del intervalo es 0.
donde el intervalo como subíndice indica donde la
función es 1, fuera del intervalo es 0.
llamamos soporte el intervalo de la función donde la función sea diferente
a 0, p.ej. el soporte de ![]() es
es ![]()
si el soporte es limitado, decimos que la función tiene soporte compacto (Si queremos ser precisos matemáticamente, la definición de soporte compacto no es tan simple.)
necesitamos un producto escalar en el espacio de las funciones, usamos el producto escalar estándar:
dos vectores son ortogonal siempre cuando
![]()
definimos un nuevo espacio vectorial ![]() que sea el complemento
ortogonal de
que sea el complemento
ortogonal de ![]() en
en ![]() , es decir,
, es decir, ![]() es el espacio
de todas las funciones en
es el espacio
de todas las funciones en ![]() que son ortogonales a todas
las funciones en
que son ortogonales a todas
las funciones en ![]() (claro, con el producto escalar eligido), es decir
(claro, con el producto escalar eligido), es decir
las funciones ![]() formando una base de
formando una base de ![]() se llama
(pre-)ondículas
se llama
(pre-)ondículas
(ondículas si también son ortogonales entre si)
obviamente,
![]() más
más
![]() forman
una base para
forman
una base para ![]()
informal significa:
las funciones ![]() en
en ![]() nos permiten representar las
partes de las funciones en
nos permiten representar las
partes de las funciones en ![]() que no se puede representar en
que no se puede representar en ![]()
las ondículas correspondientes al ejemplo de las funciones de escalado de Haar (en el contexto de nuestro espacio de funciones elegido) son
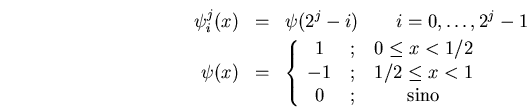
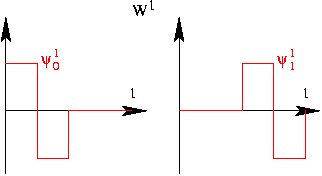
retrocemos al ejemplo
representado con funciones de escalado en ![]()
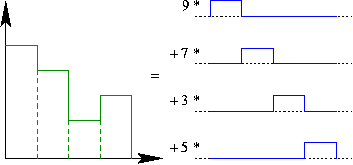
representado con funciones de escalado en ![]() más ondículas en
más ondículas en ![]()
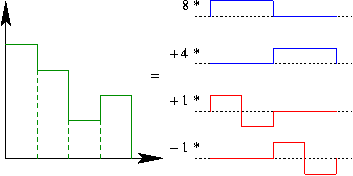
y ahora reescribimos también ![]() con
con ![]() más
más ![]()
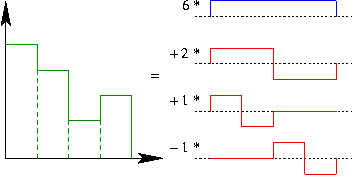
es decir, los coeficientes para representar la imagen están tomados de la combinación lineal de funciones de la secuencia de espacios