Normalización

los vectores de las bases de los espacios se puede normalizar, es decir,

$$\langle u,u\rangle =1$$

para conseguirlo con las funciones de escalado y las ondículas añadimos un factor correspondiente:

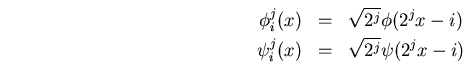
$$\begin{eqnarray*} \phi_i^j(x)&=&\sqrt{2^j}\phi(2^jx-i) \\ \psi_i^j(x)&=&\sqrt{2^j}\psi(2^jx-i) \end{eqnarray*}$$

$\phi$ y $\psi$ quedan como antes

(verifica que ahora son normales!)

como consecuencia tenemos que dividir los coeficientes con índice superior $j$ por $\sqrt{2^j}$

$$[\quad 6 \quad 2 \quad 1 \quad {-1} \quad ]\longrightarrow ... ...quad \frac{1}{\sqrt{2^1}} \quad \frac{-1}{\sqrt{2^1}} \quad ]$$