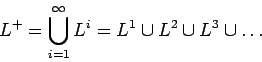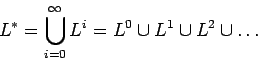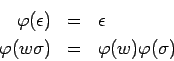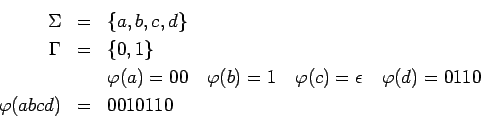Siguiente: Producciones y Derivaciones
Subir: Conceptos básicos
Anterior: Palabras
Índice General
Un lenguaje es cualquier subconjunto del universo sobre
algún alfabeto, es decir,
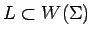 , o también
, o también
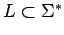 .
.
Ejemplo:
- Lenguajes triviales
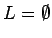 es el lenguaje vacio (que no contiene ninguna palabra),
es el lenguaje vacio (que no contiene ninguna palabra),
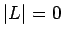
-
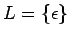 es el lenguaje que solamente contiene la palabra vacio,
es el lenguaje que solamente contiene la palabra vacio,
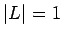
son independientes del alfabeto y por eso son lenguajes
sobre cualquier alfabeto.
- sea
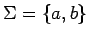
-
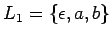
-
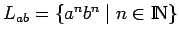 es decir, el lenguaje que contiene
todas las palabras con un número de
es decir, el lenguaje que contiene
todas las palabras con un número de 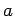 s seguidos por el mismo número
de
s seguidos por el mismo número
de 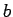 s.
s.
-
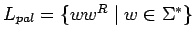 es decir, palíndromos
es decir, palíndromos
-
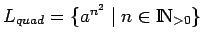
Si 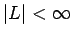 para un lenguaje
para un lenguaje
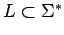 , entonces se
llama
, entonces se
llama  lenguaje finito.
lenguaje finito.
Operaciones sobre/con lenguajes,
sean
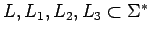 lenguajes (igual para
lenguajes (igual para 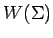 ):
):
- Unión:
-
Propiedades (unos ejemplos):
| Conmutatividad: |
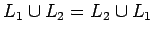 |
| Asociatividad: |
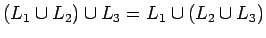 |
| Idempotencia: |
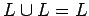 |
Operación con 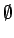 : : |
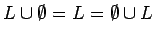 |
Operación con
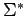 : : |
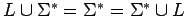 |
- Intersección:
-
Propiedades (unos ejemplos):
| Conmutatividad: |
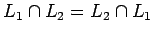 |
| Asociatividad: |
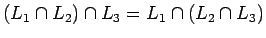 |
| Idempotencia: |
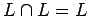 |
Operación con 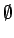 : : |
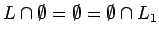 |
Operación con
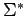 : : |
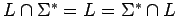 |
- Complemento:
-
Propiedades (unos ejemplos):
| Regla de DeMorgan: |
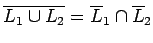 |
| |
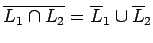 |
Con estas tres operaciones la estructura
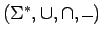 forma una álgebra booleana.
forma una álgebra booleana.
- Diferencia:
-
Propiedades (unos ejemplos):
- Concatenación:
-
Propiedades (unos ejemplos):
| No-Conmutatividad: |
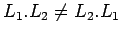 (en general) (en general) |
Operación con 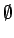 : : |
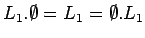 |
Operación con 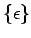 : : |
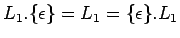 |
- Potencia:
-
Propiedades (unos ejemplos):
| Cero-Potencia: |
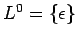 |
| Inducción: |
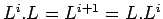 |
- Clausura positiva:
-
- Clausura (de Kleene):
-
Propiedades (unos ejemplos):
- Reflexión (o inverso):
-
- Homomorfismo:
- Sean
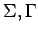 dos alfabetos.
Sea
dos alfabetos.
Sea
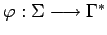 una función
que asigna a cada símbolo de
una función
que asigna a cada símbolo de 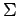 una palabra sobre
una palabra sobre 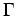 .
Podemos ampliar la función
.
Podemos ampliar la función 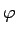 a un homomorfismo
a un homomorfismo
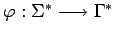 , es decir, una función que asigna a cada
palabra sobre
, es decir, una función que asigna a cada
palabra sobre 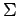 una palabra sobre
una palabra sobre 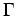 , con
, con
Ejemplo:
Entonces si
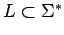 es un lenguaje sobre
es un lenguaje sobre 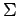
es un lenguaje sobre 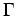 y
si
y
si
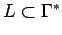 es un lenguaje sobre
es un lenguaje sobre 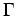 , entonces
, entonces
es un lenguaje sobre 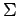 .
.
¿Cuál es el orden de prioridad de estos operadores?




Siguiente: Producciones y Derivaciones
Subir: Conceptos básicos
Anterior: Palabras
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() , o también
, o también
![]() .
.
![]() para un lenguaje
para un lenguaje
![]() , entonces se
llama
, entonces se
llama ![]() lenguaje finito.
lenguaje finito.
![]() lenguajes (igual para
lenguajes (igual para ![]() ):
):
![]() forma una álgebra booleana.
forma una álgebra booleana.