



Siguiente: Lenguajes
Subir: Conceptos básicos
Anterior: Alfabetos
Índice General
Una secuencia finita de símbolos de un alfabeto es una palabra
sobre dicho alfabeto.
Escribimos la palabra vacía,
es decir, la palabra que no contiene ningún símbolo, como 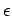 .
.
- Usamos normalmente letras minúsculas para anotar palabras,
preferiblemente desde el final del alfabeto.
- El símbolo
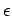 no pertenece a ningún alfabeto,
no pertenece a ningún alfabeto,
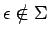
La longitud de una palabra sobre un alfabeto es el número de
símbolos que contiene.
- Dependiendo del alfabeto puede resultar difícil dividir una
palabra en sus símbolos.
- Si se puede dividir todas las palabras sobre un alfabeto solamente de
una manera en sus símbolos, se llama tal alfabeto libre.
- Solemos usar solamente alfabetos libres.
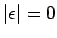
El conjunto de todas las palabras que se pueden formar sobre un
alfabeto 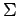 más la palabra vacía se llama el universo del alfabeto
más la palabra vacía se llama el universo del alfabeto 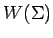 .
.
-
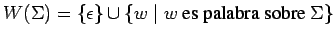
-
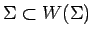
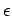 es palabra de cualquier universo,
es palabra de cualquier universo,
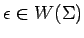 .
.
- La cardinalidad del universo es infinito (pero contable o enumerable,
vemos más adelante lo que significa).
- Si el alfabeto es libre (o mejor decir, un generador libre),
escribimos
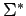 por
por 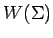 .
.
Podemos concatenar palabras, entonces
sean  ,
, 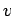 y
y 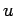 palabras en
palabras en 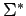 .
.
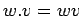 , es decir, usamos el
, es decir, usamos el  como símbolo de
concatenación, pero muchas veces obviamos de él (igual como
se suele hacer con el
como símbolo de
concatenación, pero muchas veces obviamos de él (igual como
se suele hacer con el 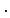 de la multiplicación).
de la multiplicación).
-
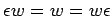 , es decir,
, es decir, 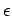 se comporta
como el elemento neutro (o elemento de intentidad)
respecto a la concatenación.
se comporta
como el elemento neutro (o elemento de intentidad)
respecto a la concatenación.

 para cualquier
para cualquier  y
y 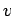 , por ejemplo:
, por ejemplo:
es decir, la concatenación no es conmutativa.
-
 para cualquier palabras
para cualquier palabras  ,
, 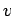 y
y 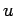 , por ejemplo:
, por ejemplo:
es decir, la concatenación es asociativa (usamos arriba las
paréntesis como metasímbolos).
- Con dichas propiedades la estructura algebraica
 forma un monoide libre (es decir, un semigrupo con elemento de intentidad).
forma un monoide libre (es decir, un semigrupo con elemento de intentidad).
Si 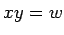 , llamamos
, llamamos 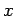 prefijo de
prefijo de  e
e 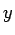 sufijo
de
sufijo
de  .
.
- Por
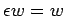 y
y 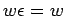 ,
, 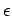 es por lo tanto prefijo
y sufijo (trivial) de cualquier palabra,
y
es por lo tanto prefijo
y sufijo (trivial) de cualquier palabra,
y  es prefijo y sufijo trivial de si mismo.
(Normalmente no consideramos estos casos triviales.)
es prefijo y sufijo trivial de si mismo.
(Normalmente no consideramos estos casos triviales.)
- Si
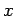 es prefijo de
es prefijo de  entonces
entonces 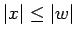 .
.
- Si
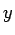 es sufijo de
es sufijo de  entonces
entonces 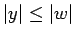 .
.
- Si
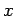 es prefijo de
es prefijo de  , e
, e 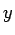 es sufijo de
es sufijo de  y
y 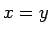 ,
entonces
,
entonces 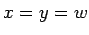 , ¿es verdad?
, ¿es verdad?
Si concatenamos siempre la misma palabra  , obtenemos potencias
de
, obtenemos potencias
de  .
.
La reflexión de una palabra  (o la palabra reversa)
anotamos como
(o la palabra reversa)
anotamos como 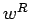 .
.




Siguiente: Lenguajes
Subir: Conceptos básicos
Anterior: Alfabetos
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática


![]() .
.
![]() más la palabra vacía se llama el universo del alfabeto
más la palabra vacía se llama el universo del alfabeto ![]() .
.
![]() ,
, ![]() y
y ![]() palabras en
palabras en ![]() .
.

![]() , llamamos
, llamamos ![]() prefijo de
prefijo de ![]() e
e ![]() sufijo
de
sufijo
de ![]() .
.
![]() , obtenemos potencias
de
, obtenemos potencias
de ![]() .
.
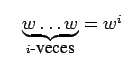 ,
,
![]() (o la palabra reversa)
anotamos como
(o la palabra reversa)
anotamos como ![]() .
.