Siguiente: Equivalencia entre AFPNDs y
Subir: Autómatas finitos con pila
Anterior: Autómatas finitos con pila
Índice General
Para cada AFPND  que acepta con pila vacía existe un AFPND
que acepta con pila vacía existe un AFPND 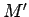 que acepta en estado final.
que acepta en estado final.
Idea de la comprobación:
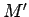 simula
simula 
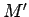 usa un nuevo símbolo
usa un nuevo símbolo 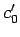 como símbolo
inicial de la pila
como símbolo
inicial de la pila
- si después de la simulación de
 dicho
dicho 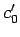 está
en la cima de la pila,
está
en la cima de la pila, 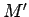 sabe que
sabe que  hubiese aceptado, es decir,
hubiese aceptado, es decir,
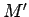 acepta también yiendo a un estado final.
acepta también yiendo a un estado final.
Para el ejemplo de antes
con el siguiente autómata que acepta con pila vacía
obtenemos el nuevo autómata que acepta en estado final

En general:
con
-
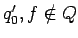 , es decir, son nuevos estados
, es decir, son nuevos estados
-
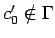 , es decir, es un nuevo símbolo inicial
, es decir, es un nuevo símbolo inicial
-
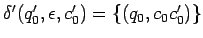 ,
es decir, la primera transición apila el antiguo símbolo inicial
y se va al antiguo estado inicial sin leer nada de la entrada
,
es decir, la primera transición apila el antiguo símbolo inicial
y se va al antiguo estado inicial sin leer nada de la entrada
-
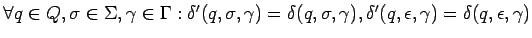 , es decir,
se simula
, es decir,
se simula 
-
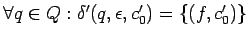 , es decir,
si la pila solamente contiene el nuevo símbolo inicial se va al
estado final.
, es decir,
si la pila solamente contiene el nuevo símbolo inicial se va al
estado final.
Para cada AFPND  que acepta en estado final existe un AFPND
que acepta en estado final existe un AFPND 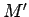 que acepta con pila vacía.
que acepta con pila vacía.
Idea de la comprobación:
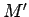 simula
simula 
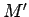 vacía desde cualquier estado final de
vacía desde cualquier estado final de  su pila
su pila
- tenemos que tener cuidado si
 no termina en estado final, pero
su pila está vacía: colocamos antes de la simulación un nuevo
símbolo
no termina en estado final, pero
su pila está vacía: colocamos antes de la simulación un nuevo
símbolo 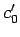 como
símbolo inicial en la pila que no `se toca' durante la simulación de
como
símbolo inicial en la pila que no `se toca' durante la simulación de  .
.
Para el ejemplo
con el siguiente autómata que acepta en estado final

(Primero observamos la consecuencia de la definición de un cálculo:
entonces, si sobran 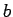 's la pila estará vacía y no habrá transición
ninguna, y por eso no llegamos a
's la pila estará vacía y no habrá transición
ninguna, y por eso no llegamos a 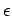 con la entrada.)
con la entrada.)
Siguiendo la idea, obtenemos el nuevo autómata que acepta con pila vacía
En general:
con
-
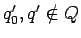 , es decir, son nuevos estados
, es decir, son nuevos estados
-
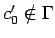 , es decir, es un nuevo símbolo inicial
, es decir, es un nuevo símbolo inicial
-
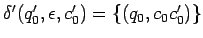 ,
es decir, la primera transición apila el antiguo símbolo inicial
y se va al antiguo estado inicial sin leer nada de la entrada
,
es decir, la primera transición apila el antiguo símbolo inicial
y se va al antiguo estado inicial sin leer nada de la entrada
-
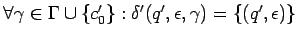 , es decir,
una vez en estado
, es decir,
una vez en estado 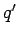 se vacía la pila sin modificar la entrada
se vacía la pila sin modificar la entrada
-
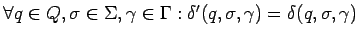 , es decir,
pasos normales de la simulación
, es decir,
pasos normales de la simulación
-
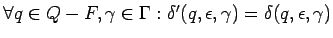 , es decir,
se simula también las transiciones
, es decir,
se simula también las transiciones 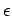 mientras
mientras  no esté
en estado final
no esté
en estado final
-
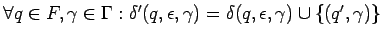 , es decir, saltamos al estado que vacía la
pila si ya estamos en estado final
, es decir, saltamos al estado que vacía la
pila si ya estamos en estado final




Siguiente: Equivalencia entre AFPNDs y
Subir: Autómatas finitos con pila
Anterior: Autómatas finitos con pila
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() que acepta con pila vacía existe un AFPND
que acepta con pila vacía existe un AFPND ![]() que acepta en estado final.
que acepta en estado final.
![]()
![]()
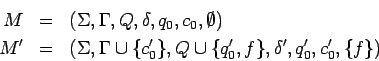
![]() que acepta en estado final existe un AFPND
que acepta en estado final existe un AFPND ![]() que acepta con pila vacía.
que acepta con pila vacía.
![]()
![]()