Un autómata finito con pila no-determinista (AFPND) es una séptupla
Es decir, el comportamiento del autómata depende en cada transición
Para el ejemplo de arriba obtenemos el autómata

También podemos dibujar autómatas con pila, por ejemplo de la siguiente manera:
![]()
Es decir, dibujamos el grafo parecido como lo hemos hecho para los
AFND-![]() : los vértices del grafo representan los estados
del autómata y las aristas representan las transiciones.
Ampliamos las etiquetas de las aristas con los
cambios en la cima de la pila.
: los vértices del grafo representan los estados
del autómata y las aristas representan las transiciones.
Ampliamos las etiquetas de las aristas con los
cambios en la cima de la pila.
Podemos pensar de un autómata con pila como un dispositivo que lee desde una cinta con símbolos, realiza cambios de estados internamente, y maneja una pila de la forma descrita:
![]()
Otro ejemplo; construimos un AFP para el lenguaje
Idea:
Un AFPND será el siguiente:
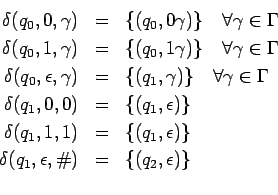
![]()
¿Cómo comprobamos que es correcto?
Dado que el contenido de la pila influye en el comportamiento del autómata necesitamos una notación para describir los cálculos del autómata.
La configuración (o descripción instantánea) ![]() de un AFP
de un AFP
![]() es la tripla
es la tripla ![]() donde
donde
Si el autómata está en configuración ![]() podemos definir que es una
posible siguiente configuración, es decir, después de haber realizado
un paso en el cálculo.
podemos definir que es una
posible siguiente configuración, es decir, después de haber realizado
un paso en el cálculo.
![]() es configuración sucesora
de
es configuración sucesora
de
![]() (es decir,
(es decir, ![]() es el siguiente
símbolo de la entrada y
es el siguiente
símbolo de la entrada y ![]() la cima de la pila),
si
la cima de la pila),
si
![]() y, para las transiciones
y, para las transiciones ![]() ,
,
![]() es configuración sucesora
de
es configuración sucesora
de
![]() (es decir, no se lee un
símbolo de la entrada y
(es decir, no se lee un
símbolo de la entrada y ![]() la cima de la pila),
si
la cima de la pila),
si
![]() .
.
Observa, si la pila está vacía, no existe configuración sucesora ninguna.
Escribimos
![]() si
si ![]() es configuración sucesora
de
es configuración sucesora
de ![]() .
Si existe una secuencia de configuraciones sucesoras de
.
Si existe una secuencia de configuraciones sucesoras de ![]() hasta
hasta ![]() ,
es decir,
,
es decir,
Un AFPND acepta una palabra ![]() de entrada según modus:
de entrada según modus:
El lenguaje aceptado por un autómata AFPND ![]() es
es
En la siguiente sección comprobamos que ambos métodos de aceptación son equivalentes para los AFPND (pero no será el caso de ls AFPD, los autómatas finitos con pila deterministas, que veremos más adelante).
Comprobamos ahora que el ![]() es correcto, es decir, tenemos
que comprobar que
es correcto, es decir, tenemos
que comprobar que
![]() .
.
Primero verificamos que ![]() acepta para cualquier palabra
acepta para cualquier palabra
![]() la palabra
la palabra ![]() :
:
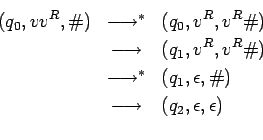
Luego comprobamos que ![]() solamente acepta palabras en
solamente acepta palabras en ![]() .
.
(por incluir)