



Siguiente: Autómatas finitos con pila
Subir: Autómatas finitos con pila
Anterior: Autómatas finitos con pila
Índice General
Ya sabemos
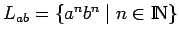 no es regular (comprobamos
con el lema de bombeo o con el teorema de Myhill-Nerode).
no es regular (comprobamos
con el lema de bombeo o con el teorema de Myhill-Nerode).
Pero 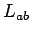 es libre de contexto con la siguiente gramática:
es libre de contexto con la siguiente gramática:
Otro ejemplo parecido es: expresiones matemáticamente correctas
de diferentes tipos de paréntesis
![$\Sigma_T=\{[,],\langle,\rangle,(,)\}$](img848.gif) ,
por ejemplo,
,
por ejemplo,
![$( ( ] ] ) \rangle )$](img849.gif) es incorrecto y
es incorrecto y
![$[ ( [ ] ) \langle ( ) \rangle ]$](img850.gif) es correcto.
es correcto.
es libre de contexto, con el sistema de producciones
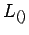 no es regular, porque ya
no es regular, porque ya ![$[^n]^n$](img854.gif) no es regular.
no es regular.
¿Podemos construir un tipo de autómata que acepta una
palabra de 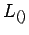 ?
?
Idea: usamos una pila para memorizar lo que se ha leído:
- Las paréntesis que abren ponemos en la pila.
- Si vemos una parentesis que cierre la cima de la pila tiene que
ser su homóloga y la quitamos de la pila.
- Al final, la pila tiene que estar vacía.
Eso era bastante fácil, ampliamos las posibilidades algo más, permitimos
- que el autómata pueda tener varios (número finito)
estados (parecido a los AFD, pero veremos que basta con un estado);
- que el autómata sea no-determinista
(veremos que habrá una diferencia entre AFPDs y AFPNDs);
- que exista la posibilidad de transiciones
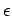 ;
;
- que acepte con pila vacía o con estados finales
(veremos que ambas formas son equivalentes);
- que existan más símbolos para la pila;
- que se apile más de un símbolo a la vez;
- que se disponga de un símbolo inicial en la pila.




Siguiente: Autómatas finitos con pila
Subir: Autómatas finitos con pila
Anterior: Autómatas finitos con pila
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() no es regular (comprobamos
con el lema de bombeo o con el teorema de Myhill-Nerode).
no es regular (comprobamos
con el lema de bombeo o con el teorema de Myhill-Nerode).
![]() es libre de contexto con la siguiente gramática:
es libre de contexto con la siguiente gramática:
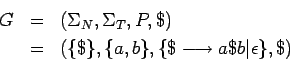
![]() ,
por ejemplo,
,
por ejemplo,
![]() es incorrecto y
es incorrecto y
![]() es correcto.
es correcto.
![]() no es regular, porque ya
no es regular, porque ya ![]() no es regular.
no es regular.
![]() ?
?