Equivalencia entre AFPNDs y gramáticas libres de contexto

Para cada gramática libre de contexto $G$ existe un autómata finito con pila no-determinista $M$ que acepta el mismo lenguaje, es decir, $L(M)=L(G)$.

La comprobación es constructiva.

Sea $G=(\Sigma_T,\Sigma_N,P,\$)$ una gramática libre de contexto.

Podemos convertir la gramática en su forma normal de Greibach (FNG), es decir todas las producciones son del tipo: $A\longrightarrow \sigma\Upsilon$ con $\sigma\in\Sigma_T$ y $\Upsilon\in\Sigma_N^*$ o la producción es $\$\longrightarrow \epsilon$ si $\epsilon\in L(G)$.

Construimos un AFPND $M=(\Sigma_T,\Sigma_N,\{q\},\delta,q,\$,\emptyset)$, (es decir, con un sólo estado) que acepta con pila vacía, donde

$$(q,\Upsilon)\in\delta(q,\sigma,A)$$

siempre que $A\longrightarrow \sigma\Upsilon$ sea una producción en $P$ y

$$(q,\$)\in\delta(q,\epsilon,\epsilon)$$

siempre que $\$\longrightarrow \epsilon$ sea una producción en $P$.

Entonces, el autómata simula en un cálculo la aplicación de las reglas de la gramática siempre siguiendo la derivación más a la izquierda para la palabra en cuestión.

Ejemplo:

$$G=(\{a,b\},\{\$,A,B,C\},P,\$)$$

con

$$P=\{\$\longrightarrow aBBC,A\longrightarrow aAA\vert b,B\longrightarrow bBAC\vert b,C\longrightarrow b\}$$

que ya está en forma formal de Greibach, entonces el AFPND es:

$$M=(\{a,b\},\{\$,A,B,C\},\{q\},\delta,q,\$,\emptyset)$$

con

$$\begin{eqnarray*} \delta(q,a,\$) &=& \{(q,BBC)\}\\ \delta(q,a,A) &=& \{(q,AA)\}... ...{(q,BAC),(q,\epsilon)\}\\ \delta(q,b,C) &=& \{(q,\epsilon)\}\\ \end{eqnarray*}$$

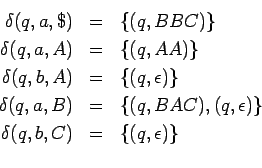
Para cada autómata finito con pila no-determinista $M$ existe una gramática libre de contexto $G$ que genera el mismo lenguaje, es decir, $L(G)=L(M)$.

La comprobación es constructiva.

Sea $M=(\Sigma,\Gamma,Q,\delta,q_0,c_0,F)$ un AFPND.

Si $F\not=\emptyset$ podemos convertir el autómata en un AFPND que acepte con pila vacía.

Luego podemos asumir que todas las transiciones del autómata como mucho apilan dos símbolos a la pila, porque podemos introducir estados intermedios que apilan poco a poco todos los símbolos necesarios sin leer más de la entrada, en concreto,

• sea $(q,v)\in\delta(p,\sigma,\gamma)$ con $v=\gamma_1\gamma_2\dots\gamma_k$, $\sigma\in\Sigma$, y $k>2$ una transición de tal tipo
• añadimos los nuevos estados $q_1,q_2,\dots,q_{k-2}$ a $Q$ y sustituimos la transición por
  $$\begin{eqnarray*} (q_1,\gamma_{k-1}\gamma_k) &\in& \delta(p,\sigma,\gamma) \\ (... ...(q,\gamma_1\gamma_2) &\in& \delta(q_{k-2},\epsilon,\gamma_2) \\ \end{eqnarray*}$$
  
  

• Observa que podemos realizar tal sustitución igual en caso que el autómata ejecute una transición-$\epsilon$ (es decir, arriba no se lee $\sigma$ de la entrada sino $\epsilon$); entonces, para simplificar escribimos $\sigma^\prime$ si leemos o bien un símbolo $\sigma\in\Sigma$ o bien $\epsilon$.

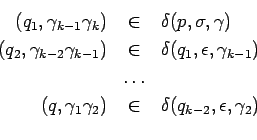
Entonces, asumimos que tengamos un AFPND que acepta con pila vacía y que apile en una transición como mucho dos símbolos a la vez.

Construimos una gramática libre de contexto $G=(\Sigma,\Sigma_N,P,\$)$, es decir, con los mismos símbolos de entrada, y donde

• $\Sigma_N$ está formado por las triplas $[p,A,q]$ siendo $p,q\in Q$ y $A\in\Gamma$, y el símbolo $\$.
• $P$ es el conjunto de producciones donde añadimos
  • para cada estado $q\in Q$ las reglas $\$\longrightarrow [q_0,c_0,q]$
  • para cada transición $(q,\epsilon)\in\delta(p,\sigma^\prime,\gamma)$ la regla $[p,\gamma,q]\longrightarrow \sigma^\prime$
  • para cada transición $(q,\gamma_1)\in\delta(p,\sigma^\prime,\gamma)$ y cada estado $r\in Q$ las reglas $[p,\gamma,r]\longrightarrow \sigma^\prime[q,\gamma_1,r]$
  • para cada transición $(q,\gamma_1\gamma_2)\in\delta(p,\sigma^\prime,\gamma)$ y cada par de estados $r,s\in Q$ las reglas $[p,\gamma,r]\longrightarrow \sigma^\prime[q,\gamma_1,s][s,\gamma_2,r]$
• observa que pueden existir reglas nulas en caso que $\sigma^\prime=\epsilon$

Entonces, la gramática simula un cálculo del autómata con una derivación más a la izquierda para la palabra en cuestión.

Formalmente hay que comprobar la equivalencia

$$\$\longrightarrow ^*w\Longleftrightarrow (q_0,w,c_0)\shortmid\joinrel\relbar\joinrel\relbar ^*(q,\epsilon,\epsilon)$$

es decir, si existe una derivación también existe un cálculo y al revés.

La comprobación del lado izquierdo al lado derecho se realice mediante una inducción sobre la longitud de una derivación más a la izquierda y la otra dirección mediante una inducción sobre la longitud del cálculo. El caso inicial, es decir, se aplica solamente una regla o se calcula solamente una configuración siguiente, se verifica directamente a partir de la construcción.

• Juntas ambas direcciones nos proporcionen la equivalencia entre las gramáticas libres de contexto y los autómatas finitos con pila no-deterministas.
• En la primera parte de la comprobación observamos que basta un solo estado en un AFPND (si un AFPND tiene más estados, podemos construir una gramática equivalente, y después un AFPND con un solo estado).
• En la segunda parte de la comprobación observamos que basta con una gramática en forma normal de Greibach donde las producciones tengan como mucho 2 símbolos no-terminales en sus partes derechas (es decir, también en la FNG los árboles de derivación pueden ser árboles binarios como en la FNC).