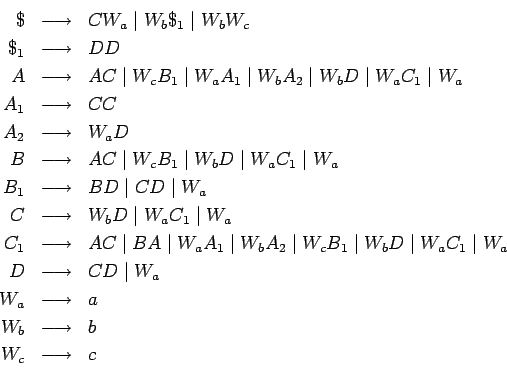Siguiente: Lema de bombeo para
Subir: Lenguajes libres de contexto
Anterior: Forma Normal de Chomsky
Índice General
Forma Normal de Greibach
Veremos otra posible normalización de gramáticas que nos sirve
más adelante para construir cierto tipo de autómatas.
Una gramática es en forma normal de Greibach (FNG) si
 (es decir, su
(es decir, su  ) solamente contiene variables útiles
) solamente contiene variables útiles
- todas las producciones de
 (es decir, en su
(es decir, en su 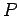 ) son de la forma
) son de la forma
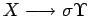 donde
donde
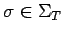 y
y
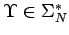 ,
es decir, todas las reglas tienen como primer símbolo en sus partes
derechas un símbolo terminal que es seguido por una palabra de variables.
,
es decir, todas las reglas tienen como primer símbolo en sus partes
derechas un símbolo terminal que es seguido por una palabra de variables.
- (porque así no se podría derivar
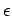 ) si
) si 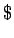 (es decir, el símbolo inicial de
(es decir, el símbolo inicial de 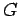 ) no aparece al lado derecho
de una producción, también está permitido que
) no aparece al lado derecho
de una producción, también está permitido que
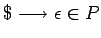
Obviamente cualquier gramática en forma normal de Greibach es una gramática
libre de contexto que se verifica directamente analizando la forma de producciones
permitidas.
Una interesante propiedad es:
para cualquier lenguaje libre de contexto
existe una gramática en forma normal de Greibach, que genera el lenguaje.
La comprobación de este hecho detallamos con la siguiente construcción,
donde a partir de una gramática libre de contexto dada elaboramos
una nueva gramática en forma normal de Greibach.
Sea  un lenguaje libre de contexto y
un lenguaje libre de contexto y
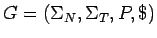 una gramática que genere
una gramática que genere  (es decir
(es decir 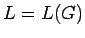 ).
).
La construcción sigue 4 pasos (asumimos que
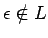 , eso
remediamos al final):
, eso
remediamos al final):
- construimos una gramática equivalente en forma normal de Chomsky
- sustituimos las reglas recursivas a la izquierda, es decir, reglas
de tipo
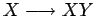
- establecemos un orden en las variables, es decir
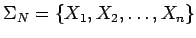 de tal manera que todas
las reglas serán de tipo
de tal manera que todas
las reglas serán de tipo
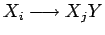 con
con  ,
, 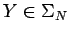
- sustituimos las reglas que no tengan un símbolo terminal
como primer símbolo en su parte derecha.
Las gramáticas después de cada paso llamamos
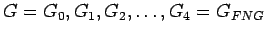 respectivamente.
respectivamente.
Usamos la misma gramática inicial como en el apartado anterior
donde 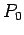 contenga las siguientes producciones:
contenga las siguientes producciones:
como ejemplo para realizar todos los pasos.
- La transformación a FNC hicimos arriba.
Entonces ya tenemos
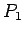 como
como
solo reordenado, para que aparezcan las partes derechas con variables
al principio al comienzo de las listas.
- Para cada producción recursiva a la izquierda, es decir, regla de tipo
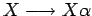 con
con 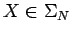 y
y
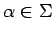 se realiza los siguientes 3 pasos:
se realiza los siguientes 3 pasos:
- se sustitue
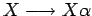 por
por
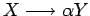 siendo
siendo 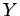 una nueva variable
una nueva variable
- se añade las reglas
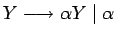
- para cada regla
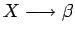 se añade
se añade
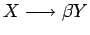 si
si 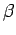 no comienza con
no comienza con 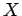
En 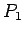 hay una regla recursiva a la izquierda:
hay una regla recursiva a la izquierda:
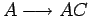 .
Entonces, la sustituimos por
.
Entonces, la sustituimos por
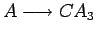 , añadimos
, añadimos
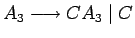 y añadimos las demás reglas para
y añadimos las demás reglas para 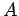 ,
y resulta el conjunto
,
y resulta el conjunto 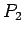 :
:
Entonces las reglas en 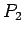 tienen de nuevo diferentes longitudes en sus
partes derechas (incluso puede ser que haya reglas unitarias).
tienen de nuevo diferentes longitudes en sus
partes derechas (incluso puede ser que haya reglas unitarias).
- (por incluir)
- (por incluir)
Dado que con una gramática en forma normal de Greibach se genera con
cada producción exactamente un símbolo terminal, cada palabra derivable
con tal gramática tiene una derivación igual a la longitud de la palabra.
Ojo, eso no significa que se puede encontrar una derivación en tiempo
lineal, porque es posible que en un momento se puede aplicar más de una
regla.




Siguiente: Lema de bombeo para
Subir: Lenguajes libres de contexto
Anterior: Forma Normal de Chomsky
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() un lenguaje libre de contexto y
un lenguaje libre de contexto y
![]() una gramática que genere
una gramática que genere ![]() (es decir
(es decir ![]() ).
).
![]() , eso
remediamos al final):
, eso
remediamos al final):
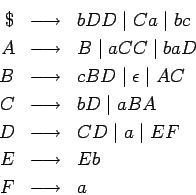
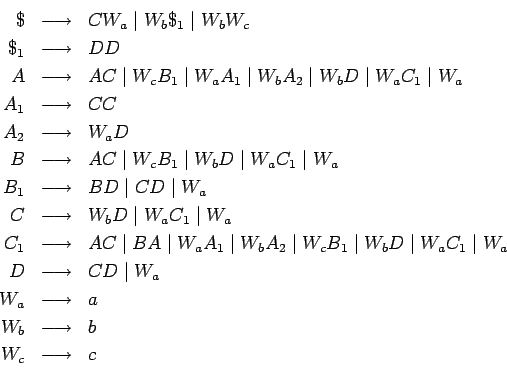
![]() hay una regla recursiva a la izquierda:
hay una regla recursiva a la izquierda:
![]() .
Entonces, la sustituimos por
.
Entonces, la sustituimos por
![]() , añadimos
, añadimos
![]() y añadimos las demás reglas para
y añadimos las demás reglas para ![]() ,
y resulta el conjunto
,
y resulta el conjunto ![]() :
: