Lema de bombeo para lenguajes libres de contexto

Siguiente: Autómatas finitos con pila Subir: Lenguajes libres de contexto Anterior: Forma Normal de Greibach Índice General

Lema de bombeo para lenguajes libres de contexto

Igual como lo hemos visto para lenguajes regulares existe una propiedad que todos los lenguajes libres de contexto cumplen:

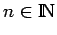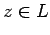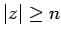Lema (de bombeo para lenguajes libres de contexto): Sea un lenguaje libre de contexto (infinito). Entonces existe un $n\in\bbbn$ de tal manera que cada palabra $z\in L$ con $\vert z\vert\geq n$ se puede dividir en cinco partes, 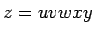cumpliéndose las tres propiedades:

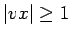
$\vert vx\vert\geq 1$
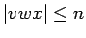
$\vert vwx\vert\leq n$
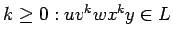
para todos los $k\geq 0: uv^kwx^ky\in L$

Idea de la comprobación:

partimos de la FNC de la gramática, es decir, las reglas son de las formas $X\longrightarrow YZ$ o $X\longrightarrow \sigma$
el árbol para una palabra (suficientemente larga) será un árbol binario
si $\vert z\vert\geq 2^{k+1}$ entonces el árbol tiene una altura por lo menos de , es decir, se encuentran variables en un camino desde la raíz hacia alguna hoja
entonces, si hay solamente variables en el alfabeto $\Sigma_N$ , se tiene que repetir una variable, sea , en un camino desde la raíz hasta una hoja
observamos los dos subárboles con dicha variable desde abajo
$\fbox{lblibre0}$
vemos: $\vert vx\vert\geq 1$ porque se tiene que derivar algo desde dado que tenemos una FNC y el árbol se bifurca en
vemos: $\vert vwx\vert\leq n$ porque la altura del subárbol hacia el segundo es como mucho
vemos: para todos los $k\geq 0: uv^kwx^ky\in L$ porque podemos eliminar y o sustituir cuantas veces como queremos el subárbol debajo de adecuadamente
$\fbox{lblibre1}$

El uso del lema de bombeo es parecido a su uso en el caso de los lenguajes regulares, se puede comprobar que ciertos lenguajes no son libres de contexto.

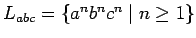Ejemplo: Investigamos $L_{abc}=\{a^nb^nc^n\;\vert\;n\geq 1\}$ .

Asumimos que 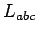$L_{abc}$ sea libre de contexto.
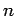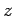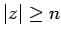El lema de bombeo nos garantiza la existencia de un tal que se cumplen las propiedades para palabras con $\vert z\vert\geq n$ . (No conocemos 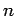en concreto, solo su existencia.)
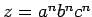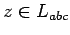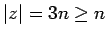(Pensamos...): Elegimos . Obviamente $z\in L_{abc}$ y $\vert z\vert=3n\geq n$ .
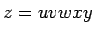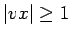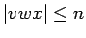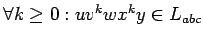El lema de bombeo nos garantiza la existencia de una partición con $\vert vx\vert\geq 1$ , $\vert vwx\vert\leq n$ , y $\forall k\geq 0: uv^kwx^ky\in L_{abc}$ . (No conocemos la partición en concreto, pero sus propiedades.)
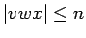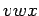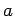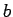(Pensamos...): Porque $\vert vwx\vert\leq n$ el no puede contener 's, 's, y 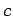's al mismo tiempo.
Entonces 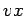tampoco, es decir, 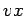contiene como mucho dos símbolos diferentes.
Porque 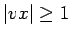$\vert vx\vert\geq 1$ la subpalabra 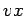contiene por lo menos un símbolo.
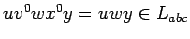$uv^0wx^0y=uwy\in L_{abc}$ pero hemos borrado como mucho dos tipos de símbolos.
Eso es una contradicción.
Entonces 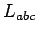$L_{abc}$ no puede ser libre de contexto.

Siguiente: Autómatas finitos con pila Subir: Lenguajes libres de contexto Anterior: Forma Normal de Greibach Índice General