



Siguiente: Forma Normal de Greibach
Subir: Lenguajes libres de contexto
Anterior: Lenguajes libres de contexto
Índice General
Forma Normal de Chomsky
Sea
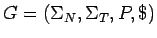 una gramática con
una gramática con
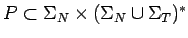 y
y 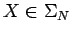 un
símbolo no-terminal (o una variable). Podemos clasificar tales
símbolos
un
símbolo no-terminal (o una variable). Podemos clasificar tales
símbolos 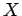 en tres clases:
en tres clases:
- variables acesibles:
- si existe una derivación desde
el símbolo inicial que contiene
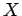 , es decir,
existe
, es decir,
existe
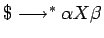 donde
donde
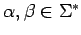 .
.
- variables generativas:
- si existe una derivación desde
el la variable que produce una sentencia
 , es decir,
existe
, es decir,
existe
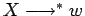 donde
donde
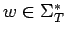 .
.
- variables útiles:
- si existe una derivación desde el símbolo inicial usando
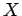 que produce una sentencia
que produce una sentencia  , es decir,
existe
, es decir,
existe
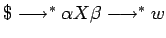 donde
donde
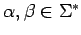 y
y
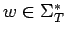 .
.
Una gramática está en forma normal de Chomsky (FNC)
- si
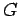 (es decir, su
(es decir, su 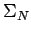 ) solamente contiene variables útiles y
) solamente contiene variables útiles y
- si todas las producciones de
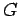 (es decir, en su
(es decir, en su 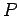 ) son
) son
- o bien de la forma
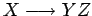 con
con
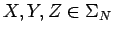
- o bien de la forma
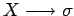 con
con 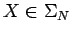 y
y
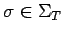
- si
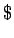 (es decir, el símbolo inicial de
(es decir, el símbolo inicial de 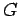 ) no aparece al lado derecho
de ninguna producción, también está permitido que
) no aparece al lado derecho
de ninguna producción, también está permitido que
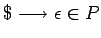 .
.
La tercera condición es necesaria para poder derivar 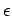 .
Si
.
Si 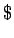 aparece a la derecha, primero habrá que sustituir las producciones
implicadas adecuadamente como lo vimos en la conversión de una gramática
lineal por la derecha a una gramática lineal por la izquierda.
aparece a la derecha, primero habrá que sustituir las producciones
implicadas adecuadamente como lo vimos en la conversión de una gramática
lineal por la derecha a una gramática lineal por la izquierda.
Observamos:
- la primera condición garantiza que todas las variables
son necesarias para derivar por lo menos una sentencia.
- la segunda condición garantiza que un árbol de
derivación es un árbol binario.
Obviamente cualquier gramática en forma normal de Chomsky es una gramática
libre de contexto que se verifica directamente analizando la forma de producciones
permitidas.
Pero también es valido la otra dirección:
para cualquier lenguaje libre de contexto
existe una gramática en forma normal de Chomsky, que genera el mismo lenguaje.
La comprobación de este hecho detallamos con la siguiente construcción
donde a partir de una gramática libre de contexto dada, elaboramos
una nueva gramática en forma normal de Chomsky.
Sea  un lenguaje libre de contexto y
un lenguaje libre de contexto y
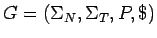 una gramática que genere
una gramática que genere  (es decir
(es decir 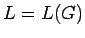 ).
).
La construcción sigue 5 pasos (asumimos que
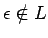 , eso
remediamos al final):
, eso
remediamos al final):
- eliminamos las variables inútiles
- modificamos las reglas para que no haya mezcla de variables
y constantes en las partes derechas de las producciones y para que todas
las reglas con constantes tengan la forma
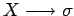
- sustituimos las reglas cuya longitud de su parte derecha es
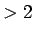
- sustituimos las reglas de tipo
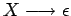
- sustituimos las reglas de tipo
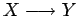 , las reglas unitarias.
, las reglas unitarias.
Las gramáticas después de cada paso llamamos
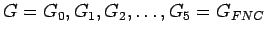 respectivamente.
respectivamente.
Usamos la siguiente gramática inicial
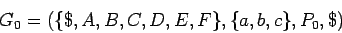
donde 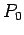 contenga las siguientes producciones:
contenga las siguientes producciones:
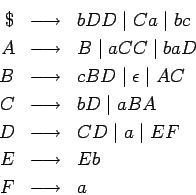
como ejemplo para realizar todos los pasos.
- Sabiendo que una variable es inútil si es no-generativa o inacesible
realizamos dos subpasos:
- eliminamos primero las variables no-generativas
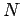 (y todas las reglas con ellas)
llamando a la gramática resultante
(y todas las reglas con ellas)
llamando a la gramática resultante 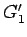 ,
,
- eliminamos después las variables inacesibles
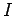 (y todas las reglas con ellas).
(y todas las reglas con ellas).
Para ello recorremos en forma estructurada las variables y reglas:
- para calcular
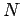 empezamos con aquellas variables que producen
directamente sentencias (incluyendo
empezamos con aquellas variables que producen
directamente sentencias (incluyendo 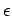 ) y seguimos el uso
de reglas con dichas variables para producir así sucesivamente sentencias
(o en otras palabras: `seguimos las reglas desde el lado derecho hacia el
lado izquierdo para obtener así la información sobre las variables').
) y seguimos el uso
de reglas con dichas variables para producir así sucesivamente sentencias
(o en otras palabras: `seguimos las reglas desde el lado derecho hacia el
lado izquierdo para obtener así la información sobre las variables').
Una forma de realizar dicho recorrido es empezar con 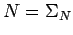 y borrar
del conjunto todas aquellas variables que o bien directamente deriven una
sentencia o bien lo hacen indirectamente.
y borrar
del conjunto todas aquellas variables que o bien directamente deriven una
sentencia o bien lo hacen indirectamente.
Se observa que solamente 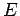 es un símbolo no-generativo, es decir,
es un símbolo no-generativo, es decir, 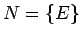 ,
,
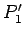 entonces es:
entonces es:
- para calcular
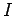 empezamos con el símbolo inicial y
veremos a cuales de
las variables se puede llegar directamente y seguimos el uso
de reglas con dichas variables para llegar así sucesivamente a nuevas
variables
(o en otras palabras: `seguimos las reglas
para obtener así la información sobre las variables acesibles').
Dicho algoritmo es una exploración de un grafo de dependencia parecido
al algoritmo que vimos para detectar estados no-acesibles en un autómata finito.
empezamos con el símbolo inicial y
veremos a cuales de
las variables se puede llegar directamente y seguimos el uso
de reglas con dichas variables para llegar así sucesivamente a nuevas
variables
(o en otras palabras: `seguimos las reglas
para obtener así la información sobre las variables acesibles').
Dicho algoritmo es una exploración de un grafo de dependencia parecido
al algoritmo que vimos para detectar estados no-acesibles en un autómata finito.
Se observa que solamente 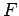 es un símbolo inacesible, es decir,
es un símbolo inacesible, es decir, 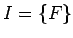 ,
,
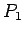 entonces es:
entonces es:
Entonces 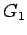 no contiene símbolos inútiles.
no contiene símbolos inútiles.
- Añadimos para cada símbolo terminal
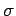 una regla
una regla
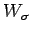 y sustituimos
y sustituimos 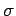 en todas las reglas de
en todas las reglas de 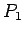 ,
,
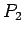 entonces es:
entonces es:
Entonces 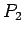 solamente contiene reglas con partes derechas siendo
solamente contiene reglas con partes derechas siendo
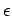 , un símbolo terminal, o una palabra de variables.
, un símbolo terminal, o una palabra de variables.
- Sustituimos cada regla del tipo
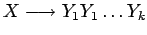 con
con
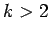 por las reglas:
por las reglas:
donde las 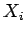 son nuevas variables,
son nuevas variables, 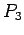 entonces es:
entonces es:
Entonces 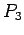 solamente contiene reglas con partes derechas siendo
solamente contiene reglas con partes derechas siendo
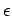 , un símbolo terminal, o una palabra de una o dos variables.
, un símbolo terminal, o una palabra de una o dos variables.
- Eliminamos las reglas que producen
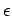 , ¡ojo!
tenemos que distinguir entre variables que solamente producen
, ¡ojo!
tenemos que distinguir entre variables que solamente producen 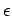 y aquellas que también producen
y aquellas que también producen 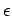 .
.
Entonces, el paso se realiza en 3 partes:
En el ejemplo tenemos:
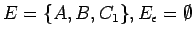 , y por eso
, y por eso
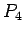 es:
es:
- Para eliminar las reglas unitarias, es decir, reglas
de tipo
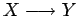 procedemos:
procedemos:
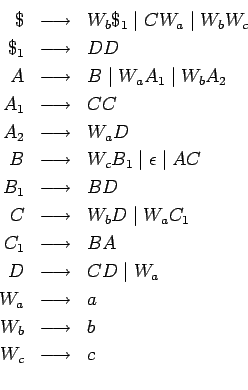
En el ejemplo tenemos:
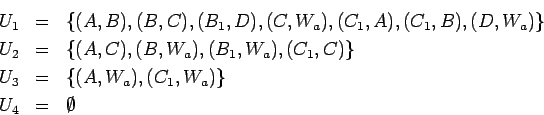
y por eso 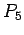 , el sistema de producciones final, queda en:
, el sistema de producciones final, queda en:
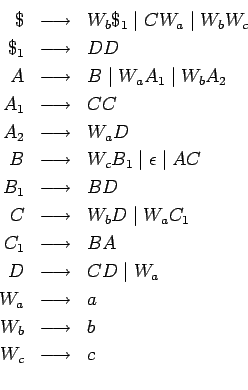
Observamos en la construcción:
- En ningún paso hemos añadido variables inútiles.
- Si hemos borrado reglas, hemos asegurado que todas las variables
siguen siendo útiles.
- Después de cada paso la gramática resultante genera el mismo
lenguaje, es decir,
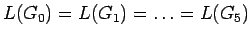 .
.
- Como se observa, la gramática
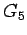 es en forma normal de Chomsky.
es en forma normal de Chomsky.
Si el lenguaje de partida  contiene la palabra vacía (
contiene la palabra vacía (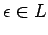 )
entonces se detecta en el pasa 4 que el símbolo inicial pertenece a
)
entonces se detecta en el pasa 4 que el símbolo inicial pertenece a 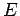 (o incluso
a
(o incluso
a 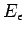 ), en este caso eliminamos con un nuevo símbolo,
por ejemplo
), en este caso eliminamos con un nuevo símbolo,
por ejemplo 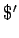 , la aparencia de
, la aparencia de 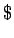 en los lados derechos y añadimos
la regla
en los lados derechos y añadimos
la regla
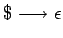 .
Tal gramática sigue estando en forma normal de Chomsky y genera
.
Tal gramática sigue estando en forma normal de Chomsky y genera
 .
.
Notas:
- El cálculo de los conjuntos
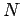 ,
, 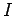 ,
, 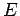 ,
, 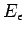 , y
, y 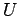 que se necesitan para sucesivamente modificar los sistemas de producciones
se realiza con un recorrido estructurado sobre las variables y producciones.
que se necesitan para sucesivamente modificar los sistemas de producciones
se realiza con un recorrido estructurado sobre las variables y producciones.
- Dado que durante el proceso hemos eliminado
producciones, puede ser que también en el alfabeto de los símbolos
terminales
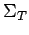 hay símbolos superfluos, es decir, que no
se pueden producir con las producciones restantes.
Dichos símbolos se pueden borrar de
hay símbolos superfluos, es decir, que no
se pueden producir con las producciones restantes.
Dichos símbolos se pueden borrar de 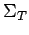 sin que se cambie el
lenguaje generado.
sin que se cambie el
lenguaje generado.
- Cuando eliminamos las reglas unitarias hemos eliminado implíctamente
las reglas innecesarias de tipo
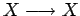 que también se podría borrar ya
antemano en un paso previo.
que también se podría borrar ya
antemano en un paso previo.
- Existen otras fuentes que primero realizan la eliminación de las reglas nulas
y de las reglas unitarias antes de demezclar y reducir las partes derechas de las reglas.
Eso es posible pero el cálculo de
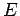 y
y 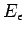 es más complejo y
las reglas de ampliación y eliminación no se limitan a dos, respectivamente tres,
casos simples como descritos arriba en el paso 4.
es más complejo y
las reglas de ampliación y eliminación no se limitan a dos, respectivamente tres,
casos simples como descritos arriba en el paso 4.




Siguiente: Forma Normal de Greibach
Subir: Lenguajes libres de contexto
Anterior: Lenguajes libres de contexto
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![]() una gramática con
una gramática con
![]() y
y ![]() un
símbolo no-terminal (o una variable). Podemos clasificar tales
símbolos
un
símbolo no-terminal (o una variable). Podemos clasificar tales
símbolos ![]() en tres clases:
en tres clases:
![]() .
Si
.
Si ![]() aparece a la derecha, primero habrá que sustituir las producciones
implicadas adecuadamente como lo vimos en la conversión de una gramática
lineal por la derecha a una gramática lineal por la izquierda.
aparece a la derecha, primero habrá que sustituir las producciones
implicadas adecuadamente como lo vimos en la conversión de una gramática
lineal por la derecha a una gramática lineal por la izquierda.
![]() un lenguaje libre de contexto y
un lenguaje libre de contexto y
![]() una gramática que genere
una gramática que genere ![]() (es decir
(es decir ![]() ).
).
![]() , eso
remediamos al final):
, eso
remediamos al final):
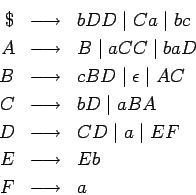
![]() y borrar
del conjunto todas aquellas variables que o bien directamente deriven una
sentencia o bien lo hacen indirectamente.
y borrar
del conjunto todas aquellas variables que o bien directamente deriven una
sentencia o bien lo hacen indirectamente.
![]() es un símbolo no-generativo, es decir,
es un símbolo no-generativo, es decir, ![]() ,
,
![]() entonces es:
entonces es:
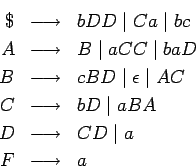
![]() es un símbolo inacesible, es decir,
es un símbolo inacesible, es decir, ![]() ,
,
![]() entonces es:
entonces es:
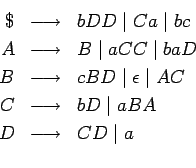
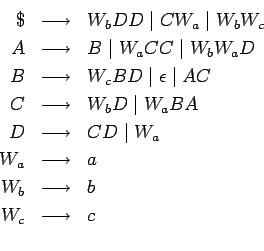
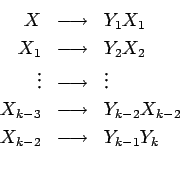
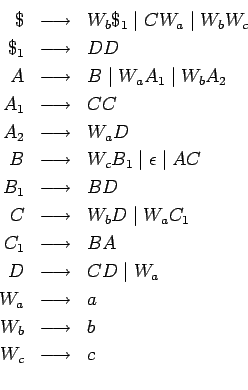
![]() , y por eso
, y por eso
![]() es:
es:
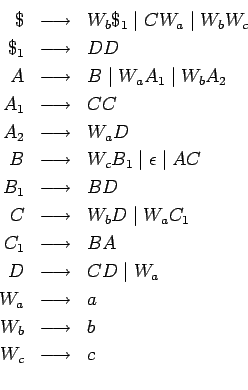
![]() vacía
para cierto
vacía
para cierto ![]() , es decir, no se ha añadido nada más.
(El índice
, es decir, no se ha añadido nada más.
(El índice ![]() de
de ![]() nos indica con cuantos `saltos' como
mucho podemos llegar.)
El algoritmo termina (porque el número de producciones es finito) y
finalmente obtenemos
nos indica con cuantos `saltos' como
mucho podemos llegar.)
El algoritmo termina (porque el número de producciones es finito) y
finalmente obtenemos
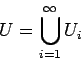
![]() en tiempo de ejecución (donde
en tiempo de ejecución (donde ![]() es el número de
nodos y
es el número de
nodos y ![]() el número de aristas en el grafo), pero algunos de ellos
se comportan en casos prácticos linealmente respecto al tamaño de
entrada (número de arista).
el número de aristas en el grafo), pero algunos de ellos
se comportan en casos prácticos linealmente respecto al tamaño de
entrada (número de arista).
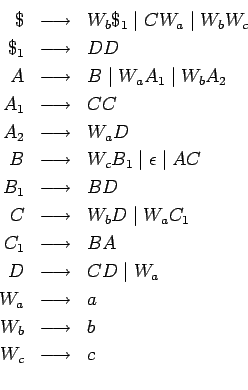
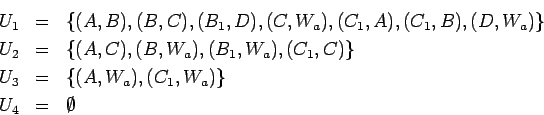
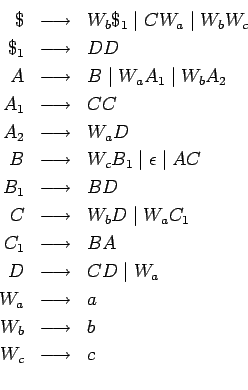
![]() contiene la palabra vacía (
contiene la palabra vacía (![]() )
entonces se detecta en el pasa 4 que el símbolo inicial pertenece a
)
entonces se detecta en el pasa 4 que el símbolo inicial pertenece a ![]() (o incluso
a
(o incluso
a ![]() ), en este caso eliminamos con un nuevo símbolo,
por ejemplo
), en este caso eliminamos con un nuevo símbolo,
por ejemplo ![]() , la aparencia de
, la aparencia de ![]() en los lados derechos y añadimos
la regla
en los lados derechos y añadimos
la regla
![]() .
Tal gramática sigue estando en forma normal de Chomsky y genera
.
Tal gramática sigue estando en forma normal de Chomsky y genera
![]() .
.