



Siguiente: Algoritmo de minimización
Subir: Autómatas finitos
Anterior: Existencia de autómatas finitos
Índice General
Investigamos de nuevo el lenguaje
anotamos unas clases de equivalencia de  :
:
verificamos que son clases de equivalencia, porque si
![$a^{k+j-1}b^j\in[a^kb]$](img475.gif) y
y
![$a^{k+l-1}b^l\in[a^kb]$](img476.gif) entonces
o bien
entonces
o bien
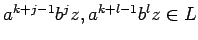 (si
(si 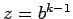 )
o bien
)
o bien
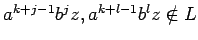 (si
(si 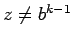 ).
).
Por eso el número de clases de 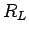 es infinito,
es decir,
es infinito,
es decir,
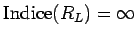 .
.
Observa que no hemos clasificado todas las palabras de
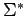 ,
sino solamente algunas palabras posibles:
,
sino solamente algunas palabras posibles:
es decir, para comprobar que un lenguaje no es regular basta con
encontrar un número infinito de clases de equivalencia (respecto a la
relación 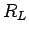 ).
).
Investigamos el lenguaje
Pensamos en las posibles clases de equivalencia.
Obviamente hay tres, o bien una palabra no termina en 0, o bien
termina en un 0, o bien termina por lo menos en dos 0, es decir:
Con
![$\mbox{$\Sigma^*$}=[\epsilon]\cup[0]\cup[00]$](img485.gif) seguimos la construcción de
arriba y obtenemos la tabla de transiciones para el autómata:
seguimos la construcción de
arriba y obtenemos la tabla de transiciones para el autómata:
o como diagrama:




Siguiente: Algoritmo de minimización
Subir: Autómatas finitos
Anterior: Existencia de autómatas finitos
Índice General
© 2006, Dr. Arno Formella, Universidad de Vigo, Departamento de Informática
![\begin{eqnarray*}[ab]&=& L \\
{}[a^2b]&=&\{a^2b,a^3b^2,a^4b^3,\dots\}\\
&\dots& \\
{}[a^kb]&=&\{a^{k+i-1}b^i\;\vert\;i\ge 1\}
\end{eqnarray*}](img474.gif)
![]() es infinito,
es decir,
es infinito,
es decir,
![]() .
.
![]() ,
sino solamente algunas palabras posibles:
,
sino solamente algunas palabras posibles:
![\begin{displaymath}\mbox{$\Sigma^*$}=L\cup
\underbrace{[a^2b]\cup\dots\cup[a^kb...
... infinito}}
\underbrace{\cup\dots}{\mbox{las dem\'as clases}}
\end{displaymath}](img482.gif)
![\begin{eqnarray*}[\epsilon]&=&\{w\;\vert\;w \mbox{ no termina en 0}\} \\
{}[0]&...
... un solo 0}\} \\
{}[00]&=&\{w\;\vert\;w \mbox{ termina en 00}\}
\end{eqnarray*}](img484.gif)
![]() seguimos la construcción de
arriba y obtenemos la tabla de transiciones para el autómata:
seguimos la construcción de
arriba y obtenemos la tabla de transiciones para el autómata:
![]()