Algoritmo de minimización

La comprobación del teorema de Myhill y Nerode nos proporciona un hecho muy importante: el autómata basado en las clases de equivalencia es el autómata mínimo dentro de todos los posibles autómatas finitos deterministas y completos que aceptan el mismo lenguaje, porque un tal autómata $M^\prime$ definiría un refinamiento de $R_{M^\prime}\subseteq R_L$, es decir, $\mathrm{Indice}(R_{M^\prime})\ge\mathrm{Indice}(R_L)$ y el AFD de las clases de equivalencia $M$ representa las mismas clases $R_L=R_M$, entonces $\mathrm{Indice}(R_{M^\prime})\ge\mathrm{Indice}(R_L)=\mathrm{Indice}(R_M)$.

Una pregunta surge: ¿Cómo sabemos si un AFD $M$ ya es mínimo?

Pues, $M$ no es mínimo, si

$$\forall w\in\mbox{$\Sigma^*$}\exists p,q\in Q, p\not= q: \delta^*(p,w)\in F \Longleftrightarrow \delta^*(q,w)\in F$$

es decir, llegamos con alguna palabra $w$ desde ambos estados siempre o bien a un estado final, o bien a un estado no-final.

En tal caso, podemos unir los dos estados en un único estado.

Basta con `realizar las pruebas' con todas las palabras $w$ con $\vert w\vert<\vert Q\vert$ porque no hace falta visitar un estado dos veces.

Con dicho argumento describimos el algoritmo de minimización (sin comprobación) a continuación.

Decimos que dos estados $p$ y $q$ son distinguibles (o no-equivalentes) si existe una palabra $w$ que nos lleva desde $p$ a un estado final pero no desde $q$, o al revés, es decir:

$$p\not\equiv q\Longleftrightarrow (\delta^*(p,w)\in F \mbox{... ...ox{ o } (\delta^*(p,w)\notin F \mbox{ y } \delta^*(q,w)\in F)$$

El algoritmo calculará la relación de distinguibilidad (o no-equivalencia) entre los estados y contiene 5 pasos.

1. Se elimina todos los estados no acesibles desde el estado inicial.
2. Se forma una tabla de todas las parejas de estados $(p,q)$ con $p\not=q$.
3. Se marca en la tabla todas las parejas $(p,q)$ con $p\in F, q\notin F$ o $p\notin F, q\in F$ (porque dichos estados seguro son distinguibles).
4. Mientras haya cambio en la tabla:

   para cada pareja $(p,q)$ no marcada y para cada símbolo 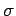$\sigma$

   si $(\delta(p,\sigma),\delta(q,\sigma))$ está marcada, también se marca $(p,q)$.

5. Las parejas (tuplas) no marcadas se une en un sólo estado.

Ejemplo: partimos del siguiente AFD completo:

1. Todos los estados son acesibles desde $a$, por eso, no hay que eliminar nada.
2. La tabla es:

   	$a$	$b$	$c$	$d$	$e$
   $a$	-
   $b$	-	-
   $c$	-	-	-
   $d$	-	-	-	-
   $e$	-	-	-	-	-

3. Las marcas iniciales son (en vez de simple marcas, usamos números para visualizar en el siguiente apartado los cambios en la tabla en cada paso):

   	$a$	$b$	$c$	$d$	$e$
   $a$	-				1
   $b$	-	-			1
   $c$	-	-	-		1
   $d$	-	-	-	-	1
   $e$	-	-	-	-	-

4. 	$a$	$b$	$c$	$d$	$e$
   $a$	-	2		3	1
   $b$	-	-	4		1
   $c$	-	-	-	5	1
   $d$	-	-	-	-	1
   $e$	-	-	-	-	-

5. El autómata mínimo es:

   

   Observa que en la construccón del autómata podemos comprobar de cierta manera la corrección de la tabla: cuando recorremos todas las aristas del autómata original, tenemos que o bien añadir o bien encontrar su homóloga en el autómata en construcción.

El paso 4 se puede implementar más eficiente. En vez de mirar tantas veces las parejas no marcados, se mantiene listas de espera que se marcan recursivamente. Observamos:

• Si tenemos que marcar $(p,q)$, es porque $(r,s)=(\delta(p,\sigma),\delta(q,\sigma))$ ya está marcado.
• Entonces de alguna manera la pareja $(p,q)$ depende de la pareja $(r,s)$.
• Es decir, si en un futuro marcamos en algun momento $(r,s)$, directamente podemos marcar $(p,q)$ también.

Para llevar eso a cabo, añadimos a cada celda una lista de parejas que dependen de la la pareja en cuestión. Si se marca una pareja, recursivamente se marcan también todas las entradas en las listas.

Con está mejora el algoritmo tiene complejidad $O(\vert Q\vert^2\vert\Sigma\vert)$.