Existencia de autómatas finitos mínimos

Ya vimos que hay varias posibilidades para construir un autómata finito determinista que acepte un lenguaje (regular), por ejemplo, por construcción directa, o por el paso de un AFND a un AFD.

Surge la pregunta: ¿existe un autómata finito determinista (AFD) mínimo que acepta tal lenguaje?

Nos referimos al número de estados que tiene el AFD, es decir $\vert Q\vert$, dado que el número de transiciones por estado está determinado por el número de símbolos en $\Sigma$ multiplicado por $\vert Q\vert$ si el AFD es completo.

La respuesta es: ¡por supuesto que sí!

Con el siguiente argumento: cada subconjunto de los números enteros $\bbbn$ tiene un mínimo, y los números de estados de todos los posibles AFDs que aceptan $L$ forman tal subconjunto.

Para la construcción del autómata mínimo necesitamos el formalismo de las relaciones de equivalencia.

Ya vimos que para cada lenguaje $L\subset \mbox{$\Sigma^*$}$ podemos construir una relación de equivalencia sobre $\mbox{$\Sigma^*$}$:

$$xR_Ly \Longleftrightarrow (\forall z\in\mbox{$\Sigma^*$}: xz\in L \Longleftrightarrow yz\in L)$$

es decir, $x$ es equivalente a $y$, si, añadiendo cualquier sufijo, ambas palabras resultantes o bien están en $L$ o bien no están en $L$.

Un lenguaje $L\subset \mbox{$\Sigma^*$}$ es regular, si y solo si el índice de la relación $R_L$ es finito, es decir, la relación tiene solamente un número finito de clases de equivalencia (Teorema de Myhill y Nerode).

Comprobamos primero la dirección `` $\Longrightarrow$'', es decir, si el lenguaje es regular, entonces el índice de la relación es finito:

$L$ es regular, entonces existe un AFD que acepta $L$.

Sea $M=(\Sigma,Q,\delta,q_0,F)$ un AFD con $L(M)=L$.

Definimos una relación de equivalencia sobre $M$:

$$xR_My\quad\mbox{si}\quad \delta^*(q_0,x)=\delta^*(q_0,y)$$

es decir, llegamos al mismo estado leyendo $x$ o $y$ empezando en el estado inicial.

Veremos a continuación que $R_M\subseteq R_L$, es decir, que $R_M$ es un refinamiento de $R_L$, o en otras palabras, si dos elementos caen en una misma clase de equivalencia respecto a la relación $R_M$, también caen en una misma clase respecto a $R_L$.

Entonces, sea $xR_My$, es decir $\delta^*(q_0,x)=\delta^*(q_0,y)$.

Sea $z\in\mbox{$\Sigma^*$}$ cualquier palabra. Miramos:

$$\begin{eqnarray*} xz\in L &\Longleftrightarrow & \delta^*(q_0,xz)\in F \\ &\Lon... ...arrow & \delta^*(q_0,yz)\in F \\ &\Longleftrightarrow & yz\in L \end{eqnarray*}$$

es decir, si $xR_My$ entonces también $xR_Ly$, y por eso:

$$\begin{eqnarray*} \mathrm{Indice}(R_L) &\le&\mathrm{Indice}(R_M)\\ &=&\mbox{n\'... ... estados acesibles desde } q_0\\ &\le&\vert Q\vert\\ &<&\infty \end{eqnarray*}$$

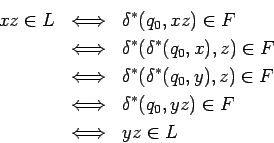
Comprobamos ahora la dirección `` $\Longleftarrow$'', es decir, si el índice de la relación es finito, entonces el languaje es regular. Dicha comprobación va a ser una comprobación constructiva muy útil:

Sea $R_L$ la relación de equivalencia de $L$ con $\mathrm{Indice}(R_L)<\infty$.

Entonces hay palabras $x_1,x_2,\dots,x_k\in\mbox{$\Sigma^*$}$ con $k<\infty$, es decir $k$ es finito, cuyas clases cubren $\mbox{$\Sigma^*$}$:

$$\mbox{$\Sigma^*$}=[x_1]\cup[x_2]\cup\dots\cup[x_k]$$

Construimos un AFD que contiene justamente tantos estados como hay clases:

$$M=(\Sigma,Q,\delta,q_0,F)$$

donde

• $Q=\{[x_1],[x_2],\dots,[x_k]\}$
• $\delta([x],\sigma)=[x\sigma]$, es decir, se hace la transición de la clase a la cual pertenece $x$ leyendo $\sigma$ a la clase a la cual pertenece $x\sigma$
• $q_0=[\epsilon]$, es decir, el estado inicial es la clase a la cual pertenece la palabra vacía
• $F=\{[x]\;\vert\;x\in L\}$, es decir, existen tantos estados finales como hay clases de equivalencia perteneciendo a $L$.

Entonces: $\delta^*([\epsilon],x)=\delta^*(q_0,x)=[x]$ y vemos

$$\begin{eqnarray*} x\in L(M) &\Longleftrightarrow & \delta^*(q_0,x)\in F \\ &\Lo... ...\Longleftrightarrow & [x]\in F \\ &\Longleftrightarrow & x\in L \end{eqnarray*}$$