Equivalencia entre AFND y AFND-$\epsilon$

Primero observamos que cualquier AFND es obviamente también un AFND-$\epsilon$ (pues uno que, por casualidad, no tenga transiciones $\epsilon$).

Luego podemos construir a partir de un AFND-$\epsilon$ un AFND equivalente.

Entonces, sea $M=(\Sigma,Q,\delta,q_0,F)$ un AFND-$\epsilon$.

Un AFND equivalente es el autómata $M^\prime=(\Sigma,Q^\prime,\delta^\prime,q_0^\prime,F^\prime)$ donde

• $Q^\prime=Q$
• $\delta^\prime(q,\sigma)=\bigcup_{r\in cl(q)} cl(\delta(r,\sigma))$ (podemos escribir solo $q$ porque $Q^\prime=Q$)
• $q_0^\prime=q_0$
• 
  
  $$F^\prime=\left\{ \begin{array}{lcl} F & \mbox{ si } & F \ca... ...box{ si } & F \cap cl(q_0)\not = \emptyset \end{array}\right.$$
  
  
  es decir, añadimos $q_0$ como estado final, si algún estado final del AFND-$\epsilon$ pertenece a la clausura-$\epsilon$ del estado inicial.

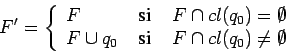
Convertimos el ejemplo:

La tabla de transiciones para $M$ con las transiciones de la clausura-$\epsilon$ es:

	$a$	$b$	$c$	$\epsilon$	$cl$
$q_0$	$\{q_0\}$	$-$	$-$	$\{q_1\}$	$\{q_0,q_1,q_2\}$
$q_1$	$-$	$\{q_1\}$	$-$	$\{q_2\}$	$\{q_1,q_2\}$
$q_2$	$-$	$-$	$\{q_2\}$	$-$	$\{q_2\}$

entonces la tabla con transiciones desde la claurura-$\epsilon$ es

	$a$	$b$	$c$	$cl$
$cl(q_0)$	$\{q_0\}$	$\{q_1\}$	$\{q_2\}$	$\{q_0,q_1,q_2\}$
$cl(q_1)$	$-$	$\{q_1\}$	$\{q_2\}$	$\{q_1,q_2\}$
$cl(q_2)$	$-$	$-$	$\{q_2\}$	$\{q_2\}$

y con eso la tabla final del AFND es

	$a$	$b$	$c$
$q_0^\prime$	$\{q_0,q_1,q_2\}$	$\{q_1,q_2\}$	$\{q_2\}$
$q_1^\prime$	$-$	$\{q_1,q_2\}$	$\{q_2\}$
$q_2^\prime$	$-$	$-$	$\{q_2\}$

Además tenemos $F \cap cl(q_0)\not=\emptyset$ y por eso $F^\prime=F\cup\{q_0\}=\{q_0,q_2\}$.

Finalmente resulta el siguiente grafo:

¿Por qué es correcto la construcción?

Pues los argumentos (y la comprobación) siguen los mismos pasos como lo vimos en el caso de AFND y AFD. Siempre cuando hay una transición en el AFND-$\epsilon$ leyendo un símbolo encontramos (según construcción) una transición en el AFND correspondiente porque consideramos toda la clausura-$\epsilon$, y vice versa, si hay una transición en el AFND, tiene que haber existido una transición en el AFND-$\epsilon$ o bien con o bien sin una secuencia de transiciones $\epsilon$.

¿Cuánto ha crecido esta vez el autómata?

El número de estados queda igual, solo se amplia (si hace falta) $F$ por un estado. Pero ha crecido el número de aristas (es decir, transisiones). Dicho crecimiento puede llegar como mucho a $\vert\Sigma\vert\vert Q\vert^2$ porque como mucho tantas aristas se pueden incorporar entre los nodos del grafo.

Finalmente hemos comprobado la equivalencia entre autómatas no-deterministas y autómatas no-deterministas con transiciones $\epsilon$.