Queremos construir un autómata que acepta el lenguaje
Si fuesemos capaz de saltar mágicamente, es decir, sin consumir una letra de la entrada, de un estado a otro, sería fácil la construcción:
![]()
Es decir, hemos introducido aristas marcados con la palabra vacía ![]() .
.
Un autómata finito no-determinista con transiciones ![]() (AFND-
(AFND-![]() ) es una quíntupla
) es una quíntupla
donde
Observamos que añadir más aristas con ![]() obviamente no
cambia el comportamiento del autómata:
obviamente no
cambia el comportamiento del autómata:
![]()
Podemos tratar las transiciones con ![]() como una relación
como una relación ![]() sobre el conjunto de estados, es decir
sobre el conjunto de estados, es decir
Esta relación podemos ampliar para que sea reflexiva, es decir,
que todas las parejas ![]() con
con ![]() formen parte de la relación,
es decir, formamos
formen parte de la relación,
es decir, formamos
Podemos ampliar la relación aun más considerando el efecto
transitivo de las transiciones ![]() , es decir, formamos en un primer paso
, es decir, formamos en un primer paso
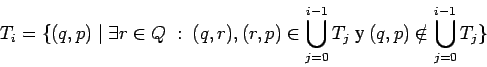
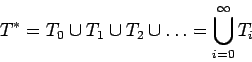
El proceso termina en nuestro caso de autómatas finitos, es decir,
la unión va solamente
sobre un número finito de ![]() s, porque
s, porque ![]() sigue siendo un subconjunto
del conjunto finito
sigue siendo un subconjunto
del conjunto finito ![]() (
(![]() ).
).
Con la clausura-![]() podemos
definir la clausura-
podemos
definir la clausura-![]() de un estado, como todos aquellos
estados que se puede alcanzar con caminos de transisiones
de un estado, como todos aquellos
estados que se puede alcanzar con caminos de transisiones ![]() , es decir
, es decir
En el ejemplo:
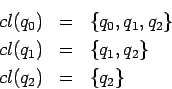
![]()
Entonces podemos formalizar el lenguaje aceptado por un
AFND-![]() (parecido a lo que hicimos para un AFND).
(parecido a lo que hicimos para un AFND).
Primero definimos la ampliación de ![]() para autómatas con
transiciones
para autómatas con
transiciones ![]() .
. ![]() va a ser
el conjunto de estados (igual como en el caso de
va a ser
el conjunto de estados (igual como en el caso de ![]() para AFNDs) que podemos alcanzar desde
para AFNDs) que podemos alcanzar desde ![]() leyendo la palabra.
Entonces:
leyendo la palabra.
Entonces:
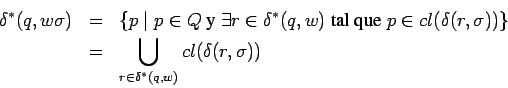
![]() enumera entonces todos los
estados alcanzables desde
enumera entonces todos los
estados alcanzables desde ![]() leyendo la palabra
leyendo la palabra ![]() .
.
Observa: Hemos dado una definición recursiva desde
la izquierda, es decir, añadimos un símbolo a la derecha.
Hubiese sido posible definir ![]() para un
AFND de la misma manera.
para un
AFND de la misma manera.
Un autómata no-determinista con transiciones ![]()
![]() acepta una palabra
acepta una palabra ![]() sobre el alfabeto
sobre el alfabeto ![]() (
(
![]() )
si
)
si
El lenguaje aceptado por ![]() es (como siempre)
es (como siempre)