Equivalencia entre AFD y AFND

Está claro que cualquier AFD también es un AFND, es decir, si $L$ es un lenguaje aceptado por un AFD, también está aceptado por un AFND. Simplemente existe como mucho una sola transición para cada símbolo del alfabeta y para cada estado.

Pero también podemos construir para cada AFND un AFD equivalente, es decir, un autómata determinsta que acepta el mismo lenguaje.

Ejemplo: convertimos el AFND que acepta $L_{dos}$ en un AFD equivalente:

Para el caso general tenemos:

Sea $M=(\Sigma,Q,\delta,q_0,F)$ un AFND, construimos un AFD $M^\prime=(\Sigma,Q^\prime,\delta^\prime,{q_0^\prime},F^\prime)$ con

• $Q^\prime\subset{\cal P}(Q)$, es decir, es--como mucho--el conjunto de todos los subconjuntos de $Q$.
• ${q_0^\prime}=\{q_0\}$, es decir, es el conjunto que contiene el estado inicial del AFND.
• $\delta^\prime(Q_i,\sigma)=P_j \Longleftrightarrow \exists q\in Q_i,p\in P_j \mbox{ con } \delta(q,\sigma)=p$, es decir, existe una transición con el símbolo $\sigma$ en el AFD, si existe alguna transición con tal símbolo entre cualquier pareja de estados correspondientes en el AFND.
• $F^\prime\subset {\cal P}(Q)$ con si $f\in F^\prime$ entonces existe un $q\in f$ con $q\in F$, es decir, el conjunto de estados finales son todos aquellos estados del AFD que contienen por lo menos un estado final del AFND.

Se suele construir los estados necesarios del AFD a lo largo de la construcción en vez de coger por defecto todos los posibles subconjuntos, para evitar--en caso que sea posible--construir muchos estados que finalmente no se alcanza desde el estado inicial.

¿Porqué es correcta la construcción?

Tenemos que comprobar formalmente que si $M$ (siendo un AFND) acepta $w$, entonces $M^\prime$ (siendo el AFD construido) también lo acepta; y si $M^\prime$ acepta $w$, entonces $M$ también lo hace, es decir, que $L(M)=L(M^\prime)$.

Pues, sea $M$ un AFND y $M^\prime$ el AFD correspondiente.

Sea $w=x_0x_1x_2\dots x_n \in L(M)$ cualquier palabra aceptada por $M$.

Comprobamos que $w\in L(M^\prime)$, es decir, $L(M)\subset L(M^\prime)$:

Definimos los siguientes diagramas

$$\begin{array}{ccc} p & \stackrel{x_{i}}{\longrightarrow } ... ...\ P & \stackrel{x_{i}}{\longrightarrow } & Q \\ \end{array}$$

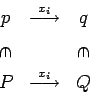
es decir, si hacemos la transición en $M$ desde $p$ a $q$ leyendo $x_i$, en otras palabras, usamos $\delta(p,x_i)=q$, entonces existe (según construcción) una transición en $M^\prime$ de $P$ (con $p\in P$) a $Q$ (con $q\in Q$) leyendo $x_i$, en otras palabras, existe $\delta(P,x_i)=Q$.

Para la palabra $w$ obtenemos:

$$\begin{array}{ccccccccccccc} q_0 & \stackrel{x_{0}}{\longr... ...}{\longrightarrow } & Q_{n+1} & \in & F^\prime \\ \end{array}$$

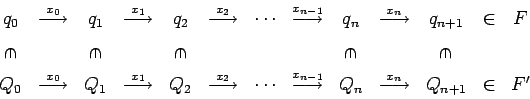
donde la construcción va desde la izquierda, es decir, del estado inicial, hacia la derecha, es decir, a un estado final. Dado que $M$ acepta $w$, $q_{n+1}$ es un estado final y siendo miembro de un conjunto $Q_{n+1}$, este será un estado final de $M^\prime$.

Entonces hemos comprobado que $M^\prime$ acepta $w$, y por eso $L(M)\subset L(M^\prime)$.

Ahora, sea $w=x_0x_1x_2\dots x_n \in L(M^\prime)$ cualquier palabra aceptada por $M^\prime$.

Comprobamos que $w\in L(M)$, es decir, $L(M)\supset L(M^\prime)$:

Definimos los siguientes diagramas

$$\begin{array}{ccc} P & \stackrel{x_{i}}{\longrightarrow } ... ...\ p & \stackrel{x_{i}}{\longrightarrow } & q \\ \end{array}$$

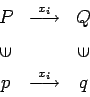
es decir, si hacemos la transición en $M^\prime$ desde $P$ leyendo $x_i$ a $Q$, en otras palabras, usamos $\delta(P,x_i)=Q$, entonces existe (según construcción) una transición en $M$ de algún $p$ (con $p\in P$) leyendo $x_i$ a algún $q$ (con $q\in Q$), en otras palabras, existe $\delta(p,x_i)=q$.

Para la palabra $w$ obtenemos:

$$\begin{array}{ccccccccccccc} Q_0 & \stackrel{x_{0}}{\longr... ...l{x_{n}}{\longrightarrow } & q_{n+1} & \in & F \\ \end{array}$$

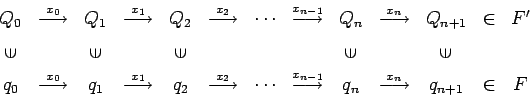
donde la construcción va ahora desde la derecha, es decir, un estado final, hacia la izquierda, es decir, al estado inicial. Dado que $M^\prime$ acepta $w$, $Q_{n+1}$ es un estado final y un conjunto no vacío, entonces existe un miembro $q_{n+1}$ que también es elemento de $F$ y por consecuencia un $q_n$ aplicando el diagrama y asi succesivamente hasta llegar a $q_0$.

Entonces hemos comprobado que $M$ acepta $w$, y por eso $L(M)\supset L(M^\prime)$.

Finalmente tenemos $L(M)\subset L(M^\prime)$ y $L(M)\supset L(M^\prime)$ y por eso $L(M)=L(M^\prime)$.

Como se observa en la construcción puede ser que se usa $2^{\vert Q\vert}$ estados en el autómata determinista si el autómata no-determinista tenía $\vert Q\vert$ estados, es decir, el crecimiento del número de estados puede ser exponencial.

Surgen dos preguntas:

¿Existen AFNDs que producen un AFD de tal tamaño grande?

¿Son necesarios tantos estados (o existe una mejor forma de realizar la conversión)?

Un ejemplo para una respuesta a la segunda:

Usamos $\Sigma=\{a,b\}$ como alfabeto. Definimos los siguientes lenguajes (que dependen del número $n\in\bbbn$):

$$L_n = \{w \;\vert\;w\in\mbox{$\Sigma^*$}, w=w_1w_2, w_1\not= w_2, \vert w_1\vert=\vert w_2\vert=n, n\in\bbbn\}$$

es decir, todas las palabras con $2n$ letras donde la primera mitad se distingue de la segunda.

Es bastante claro que para cualquier $n$ existe un autómata que acepta $L_n$ porque el lenguaje es finito ( $\vert L_n\vert=2^{2n}-2^n$).

En un libro (HotzEstenfeld) se encuentra el siguiente AFND que acepta $L_3$ (dejan la comprobación al lector)

Bueno, con un poco de trabajo se puede comprobar (enumerando todos los caminos desde el estado inicial hasta el estado final) que en cada uno de los caminos siempre existe en la primera parte una arista con una $a$ (o una $b$) donde en la misma posición de la segunda parte hay una $b$ (o una $a$).

El AFND dado tiene 22 estados que (sin que ellos lo dicen) está en el orden de $n^2$ (si inspeccionamos la construcción `vemos' la suma de 1 hasta $2n$).

También construeron un AFD para $L_3$:

Manifestan que dicho autómata es mínimo, y teniendo más de $2^n$ estados concluyen que la construcción de un AFND a un AFD puede incrementar el número de estados exponencialmente.

Veremos: ¡Ambas construcciones tienen sus deficiencias, aunque el hecho en si es correcto!

Primero, no dan un esquema cómo construir un autómata que reconozca $L_n$ para cualquier $n$ (puede ser que hay `buena suerte' en el caso de $L_3$).

Segundo, el AFD dado no es mínimo, una simplificación sería:

Pero, el nuevo autómata sigue necesitando un número exponencial de estados, porque se tiene que construir en el `lado izquierdo' todas las posibles palabras $w_1$.

Entonces: ¿Creemos o sabemos?, si no lo hemos comprobado o si no hemos entendido una comprobación presentada, entonces solamente creemos. El saber va más allá. Hay que mantenerse crítico, siempre.

Construimos un AFND para $L_n$ sistemáticamente.

Idea: En cada uno de los caminos reconociendo $w_1$ siempre tiene que existir una arista con una $a$ (o una $b$) donde en la misma posición para reconocer $w_2$ hay una $b$ (o una $a$).

Este principio nos lleva a una construcción inductiva:

El número de estados entonces es:

$$\begin{eqnarray*} \vert Q\vert&=& 1+2+4+6+\dots+2n+(2n-2)+\dots+4+2+1 \\ &=& ... ...+2\sum_{i=1}^{n-1}i \\ &=& 1+n(n+1)+1+(n-1)n \\ &=& 2(n^2+1) \end{eqnarray*}$$

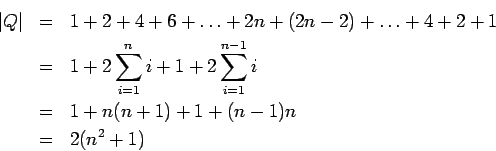
Como vemos, incluso hemos reducido el número de estados: el AFND para aceptar $L_3$ tiene solamente 20 estados.

La construcción de un AFD sigue el mismo argumento dado arriba: se necesita construir todas las posibles palabras $w_1$ en `el lado izquierdo' y por eso el AFD tiene por lo menos $2^n$ estados (los $2^n-1$ para enumerar los $w_1$ y por lo menos un estado final en `el lado derecho'.

Otro ejemplo para mostrar las capacidades de un AFND (y el crecemiento exponencial necesario del AFD equivalente):

Usamos $\Sigma=\{0,1\}$ como alfabeto. Definimos los siguientes lenguajes (que dependen del número $n\in\bbbn$):

$$L_n = \{w \;\vert\;w\in\mbox{$\Sigma^*$}, w \mbox{ contiene un 1 en la $n$-n\'esima posici\'on desde la derecha} \}$$

Es bastante fácil construir un AFND que acepte $L_n$:

No es tan obvio como construir directamente un AFD. Pero es posible con la construcción (¡Hazlo!).

Observamos en la construcción:

• Sea $w=x_nx_{n-1}\dots x_2x_1\in \{0,1\}^*$.
• Para todos los $i\in \{1,\dots, n\}$ tenemos:
  
  $$q_i\in \delta^*(q_0,w) \Longrightarrow x_i=1$$
  
  
  es decir:
  • Si $x_i=1$ (el $i$-ésimo símbolo desde la derecha es un 1), entonces existe un camino desde $q_0$ a $q_i$ (es decir, $q_i\in \delta^*(q_0,w)$) porque podemos usar dicho $x_i$ para pasar el `puente' y
  • si existe un camino desde $q_0$ a $q_i$ leyendo $w$ ( $q_i\in \delta^*(q_0,w)$), entonces $w$ tiene un 1 como $i$-ésimo símbolo desde la derecha (es decir, $x_i=1$) porque hemos pasado el `puente'.
• Entonces, existe en la construcción para cada subconjunto $P\in {\cal P}(Q)$ con $q_0\in P$ una palabra $w$ tal que tenemos que construir un camino desde $Q_0=\{q_0\}$ hacia $P$.
• Entones el AFD contiene por lo menos $2^{\vert Q\vert-1}=2^n$ estados (todos aquellos que codifican subconjuntos conteniendo $q_0$).

Construimos un AFD directamente:

Este autómata (y siguiendo el esquema de la construcción) contiene $2^n$ estados.

En ambos ejemplos parece que el número de estados necesarios en un AFD tenga algo que ver con la `capacidad de contar o enumerar' hasta cierto número.