Autómatas finitos no-deterministas (AFND)

Ampliamos un poco las posibilidades de las transiciones de un autómata finito, es decir, cambiamos la función $\delta$.

Un autómata finito no-determinista (AFND) es una quíntupla

$$M=(\Sigma,Q,\delta,q_0,F)$$

donde

• $\Sigma$ es un alfabeto.
• $Q$ es un conjunto finito no vacío de estados, es decir, $0<\vert Q\vert<\infty$.
• $\delta$ es (una de las dos definiciones, que entre si son equivalentes)
  • una relación, es decir $\delta\subset(Q\times\Sigma)\times Q$
  • o una función, es decir, $\delta\;:\;Q\times\Sigma \longrightarrow {\cal P}(Q)$ siendo ${\cal P}(Q)$ el conjunto de las partes de $Q$
  • $q_0\in Q$ es el estado inicial.
  • $F\subset Q$ es el conjunto de estados finales.

Ejemplo:un AFND para el lenguaje

$$L_{dos}=\{w\;\vert\;w\in\{0,1\}^*, w \mbox{ contiene dos 0s y dos 1s}\}$$

Representamos la función $\delta$ también con una tabla, solo que ahora aparece más de un estado en cada celda de la tabla, por eso usamos la notación de conjuntos:

$\delta$	0	1
$\Longrightarrow q_0$	$\{q_0,q_3\}$	$\{q_0,q_1\}$
$q_1$	$\emptyset$	$\{q_2\}$
$*q_2$	$\{q_2\}$	$\{q_2\}$
$q_3$	$\{q_4\}$	$\emptyset$
$*q_4$	$\{q_4\}$	$\{q_4\}$

Ampliamos de nuevo $\delta$ para definir el lenguaje aceptado por un AFND

$$\begin{eqnarray*} \delta^*:Q\times\mbox{$\Sigma^*$}&\longrightarrow & {\cal P}(Q... ...p\in\delta^*(r,w)\}\\ &&\sigma\in\Sigma, w\in\mbox{$\Sigma^*$} \end{eqnarray*}$$

es decir, $\delta^*$ coincide con $\delta$ para símbolos del alfabeto y en general enumera los estados alcanzables con tal palabra.

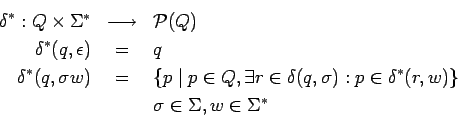
Un autómata finito no-determinista $M=(\Sigma,Q,\delta,q_0,F)$ acepta una palabra $w\in\mbox{$\Sigma^*$}$ si $\delta^*(q_0,w)\cap F\not=\emptyset$ donde $\delta^*$ es la ampliación de la relación de transición $\delta$.

O en otras palabras, $M$ acepta $w$, si $\delta^*(q_0,w)$ contiene un estado final del autómata.

El lenguaje aceptado por un autómata finito no-determinista $M$ es el conjunto de palabras aceptadas por $M$:

$$L(M)=\{w\;\vert\;w\in\mbox{$\Sigma^*$}, M \mbox{ acepta } w\}$$