Autómatas finitos deterministas (AFD)

Un autómata finito determinista (AFD) es una quíntupla

$$M=(\Sigma,Q,\delta,q_0,F)$$

donde

• $\Sigma$ es un alfabeto (sabemos $\epsilon\notin\Sigma$)
• $Q$ es un conjunto finito no vacío de estados, es decir, $0<\vert Q\vert<\infty$.
• $\delta$ es una función de transición:
  
  $$\delta:Q\times\Sigma\longrightarrow Q\;;\;\delta(q,\sigma)=p$$
  
  
  es decir, si el autómata se encuentra en el estado $q$ y `lee' el símbolo $\sigma$ va al estado $p$.
• $q_0\in Q$ es el estado inicial.
• $F\subset Q$ es el conjunto de estados finales.

Podemos pensar de un autómata como un dispositivo que lee desde una cinta con símbolos y que realiza cambios de estados internamente:

Dibujamos los autómatas como grafos dirigidos (no introducimos el concepto matemático de grafos formalmente), los estados representan los nodos del grafo, y dibujamos una arista atribuida con un símbolo entre dos nodos si existe una transisión correspondiente:

es decir, el estado inicial está marcado por una flecha y los estados finales están marcados con doble círculo.

Ejemplo: Un AFD que `acepta' las cadena de $0$s y $1$s donde los números de ceros y unos es par:

entonces

$$M=(\{0,1\},\{q_0,q_1,q_2,q_3\},\delta,q_0,\{q_0\})$$

¿Cómo describimos cómodamente $\delta$?

Observamos: $\vert Q\vert<\infty$ y $\vert\Sigma\vert<\infty$, entonces podemos hacer una tabla con los estados como filas y con los símbolos como columnas:

$$\delta(q_0,0)=q_3,\delta(q_0,1)=q_1,\delta(q_1,0)=\dots$$

o más breve una tabla:

$\delta$	$0$	$1$
$\Longrightarrow \star q_0$	$q_3$	$q_1$
$q_1$	$q_2$	$q_0$
$q_2$	$q_1$	$q_3$
$q_3$	$q_0$	$q_2$

• `Determinista' significa que no tenemos opción ninguna para eligir, $\delta$ es una función.
• Si $\delta$ es una función total llamamos el autómata completo, es decir, existe para cada estado y cada símbolo una transición.
• Abreviamos los dibujos para reducir el número de aristas:

  

  es decir, permitimos escribir más de un símbolo por arista, pero el cambio de estado se realiza con leer solo uno de la lista.

Para definir el lenguaje aceptado por un AFD ampliamos la función $\delta$ a una función $\delta^*$ para que trabaja sobre palabras:

$$\begin{eqnarray*} \delta^*:Q\times\mbox{$\Sigma^*$}&\longrightarrow & Q\\ \delt... ...\delta(q,\sigma),w)\quad \sigma\in\Sigma, w\in\mbox{$\Sigma^*$} \end{eqnarray*}$$

es decir, $\delta^*$ refleja el movimiento de la cabeza de lectura del autómata.

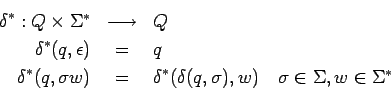
Un autómata finito determinista $M=(\Sigma,Q,\delta,q_0,F)$ acepta una palabra $w\in\mbox{$\Sigma^*$}$ si $\delta^*(q_0,w)\in F$ donde $\delta^*$ es la ampliación de la funcion de transición $\delta$.

O en otras palabras, $M$ acepta $w$, si $\delta^*(q_0,w)$ es un estado final del autómata.

El lenguaje aceptado por un autómata finito determinista $M$ es el conjunto de palabras aceptadas por $M$:

$$L(M)=\{w\;\vert\;w\in\mbox{$\Sigma^*$}, M \mbox{ acepta } w\}$$

En el grafo podemos observar: si $w\in L(M)$ entonces existe un camino en el grafo desde el estado inicial $q_0$ hasta algún estado final de tal manera que podemos `leer' la palabra $w$ a lo largo de las aristas visitadas.

Ejemplo: Un autómata que acepta números reales (en Pascal):

Curiosidades de C/C++:

• Comprueba con un compilador de C/C++ (o de Java) si a=000; o a=0011.0; son sentencias correctas, sino no lo son, modifica el autómata adecuadamente (¿Qué pasa con a=009?).
• Comprueba con un compilador de C/C++ (o de Java) si a=3E000; es una sentencia correcta, sino no lo es, modifica el autómata adecuadamente.
• a=.1+ +1.; es una sentencia correcta en C/C++ (se asigna a a el valor 1.1 siendo la suma de dos constantes flotantes), pero importante es el espacio entre los dos +

Vemos que estámos confrontados con diferentes problemas:

• deberíamos saber antemano: ¿Qué es una constante flotante?
• deberíamos traducir dicho conocimiento en un autómata
• deberíamos comprobar si dicho autómata de verdad acepta lo que debe aceptar
• si implementásemos tal autómata de forma real, deberíamos comprobar adicionalmente si la implementación refleja la descripción matemática

Observamos, cada AFD se puede completar:

• añadimos un estado $e$ a $Q$ (pero $e\notin F$)
• añadimos las transiciones que faltan, es decir, $\delta(q,\sigma)=e$ para todos los $q\in Q$ (incluyendo $e$) y $\sigma\in\Sigma$
• con eso $\delta$ se convierte en una función total

Observamos:

• si $q_0\in F$ entonces $\epsilon\in L(M)$ y al revés, si $\epsilon\in L(M)$ entonces $q_0\in F$.
• puede ocurrir que hay estados no acesibles desde $q_0$, incluso pueden ser aislados, es decir, no existe un camino desde $q_0$ hacia tal estado.

Dos autómatas $M_1$ y $M_2$ son equivalentes si aceptan el mismo lenguaje, $M_1\equiv M_2$ si $L(M_1)=L(M_2)$.

• Si eliminamos todos los estados no acesibles (o aislados) de un autómata, obtenemos un autómata equivalente al autómata original.
• Obviamente tal autómata se representa con un grafo conexo.

Dos estados $q_1$ y $q_2$ de dos autómatas $M_1$ y $M_2$ son equivalentes, es decir, $q_1\equiv q_2$, si para $q_1\in Q_1$ y $q_2\in Q_2$ $\delta^*(q_1,w)\in F_1 \Leftrightarrow \delta^*(q_2,w)\in F_2$.

Entonces dos autómatas son equivalentes si sus estados iniciales son equivalentes.