2- und 3- dimensionaler Vektorraum

Wir schreiben hier nur die 3-dimensionalen Versionen. Wir schreiben in Spaltennotation. Wir schreiben die Koordinaten eines Punktes entweder entsprechend der Namen der Koordinatenachsen, oder als eigener Namen mit Indizierung entsprechend der Koordinatenachse, also:

$$p = \left(\begin{array}{c}x\\ y\\ z\end{array}\right) \quad... ...d p = \left(\begin{array}{c}p_0\\ p_1\\ p_2\end{array}\right)$$

Vektorraum, 2- oder 3-dimensionaler Punktraum, siehe Algebra, hier nur einige Auffrischungen.

Vektoren

$${\vec x}= \left(\begin{array}{c}x_0\\ x_1\\ x_2\end{array}\right)$$

Ortsvektor eines Punktes ist der durch die Koordinaten bzgl. eines Koordinatensystems eindeutig festgelegte Vektor. Wir machen keinen wesentlichen Unterschied zwischen einem Punkt und seinem Ortsvektor.

Vektoroperationen

Vektoraddition

$${\vec x}+ {\vec y}= \left(\begin{array}{c}x_0\\ x_1\\ x_2\end... ...(\begin{array}{c}x_0+y_0\\ x_1+y_1\\ x_2+y_2\end{array}\right)$$

Skalarmultiplikation

$$\alpha{\vec x}= \alpha\left(\begin{array}{c}x_0\\ x_1\\ x_2\e... ...rray}{c}\alpha x_0\\ \alpha x_1\\ \alpha x_2\end{array}\right)$$

Standardskalarprodukt

Für zwei Vektoren ${\vec x}$ und ${\vec y}$ ist das Standardskalarprodukt gegeben als:

$$\langle{\vec x},{\vec y}\rangle = x_0y_0+x_1y_1+x_2y_2$$

Damit kann man die Länge eines Vektors und den Abstand zweier Punkte berechnen.

Länge

$$\vert{\vec x}\vert = \sqrt{\langle{\vec x},{\vec x}\rangle }$$

Abstand

$$\vert{\vec p}-{\vec q}\vert = \sqrt{\langle{\vec p}-{\vec q},{\vec p}-{\vec q}\rangle }$$

d.h. Länge des Differenzvektors. Man beachte, auch hier

Winkel zwischen zwei Vektoren

$$\cos\alpha = \frac{\langle{\vec x},{\vec y}\rangle }{\vert{\vec x}\vert\vert{\vec y}\vert}$$

Wieso stimmt dies? (Überprüfen Sie es als Übung).

Bemerkung: Man sollte die Formel nicht zur Berechnung des Winkels zwischen zwei normierten Vektoren verwenden, da einerseits durch Rundungsfehler das Skalarprodukt Werte außerhalb des Definitionsbereiches der Arcuskosinusfunktion liefern kann und andererseits gerade im Bereich $\alpha=0$ die Kosinusfunktion sehr flach verläuft, was eine exakte Berechnung numerisch erschwert. Deshalb besser:

$$\alpha = 2\cdot\arctan (\vert{\vec u}-{\vec v}\vert/\vert{\vec u}+{\vec v}\vert)$$

welches man im Zweidimensionalen z.B. durch folgendes Programmsegment berechnet:

double Angle(
  const Vector2D& u,
  const Vector2D& v
) {
  const double duv(hypot(u.x-v_x,u.y-v.y));
  const double suv(hypot(u.x+v_x,u.y+v.y));
  return 2.0 * atan2(duv,suv);
}

Vektorprodukt

$${\vec x}\times {\vec y}= \left(\begin{array}{c}x_0\\ x_1\\ x_... ..._1y_2-x_2y_1\\ x_2y_0-x_0y_2\\ x_0y_1-x_1y_0\end{array}\right)$$

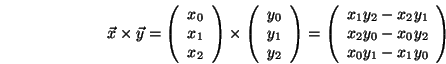
Hadamardsche Produkt

$${\vec x}\star {\vec y}= \left(\begin{array}{c}x_0\\ x_1\\ x_2... ...c}x_0\cdot y_0\\ x_1\cdot y_1\\ x_2\cdot y_2\end{array}\right)$$

Koordinatensysteme

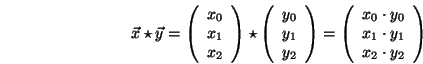
orthonormale (kartesische) Koordinatensysteme, d.h. die Basisvektoren haben Länge 1 und stehen senkrecht aufeinander:

$$e_x = \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right) \qu... ... \quad e_z = \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$$

$$\begin{eqnarray*} p &=& x e_x + y e_y + z e_z \\ &=& \left(\begin{array}{c}x\\ y\\ z\end{array}\right) \end{eqnarray*}$$

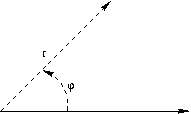
polares Koordinatensystem (2D)

ein Punkt wird durch seinen Abstand vom Ursprung und durch den Winkel mit einer gegebenen Achse (normalerweise der $x$-Achse eines darunterliegenden kartesischen Koordinatensystems) beschrieben:

$$p = \left(\begin{array}{c}r\\ \varphi\end{array}\right)$$

Kugelkoordinatensystem (3D)

ein Punkt wird durch seinen Abstand vom Ursprung und durch die Winkel bzgl. einer gegebenen Achse und Ebene (normalerweise die $z$-Achse und $xz$-Ebene eines darunterliegenden kartesischen Koordinatensystems) beschrieben:

$$p = \left(\begin{array}{c}r\\ \delta\\ \varphi\end{array}\right)$$

Hierbei ist $\delta$ der Winkel mit der $z$-Achse und $\varphi$ der negative Rotationswinkel der notwendig ist, um den Punkt mit einer Drehung um die $z$-Achse in die $xz$-Ebene zu drehen.

Es gibt noch andere Koordinatensysteme, z.B. Zylinderkoordinatensystem.

Umrechnung von einem Koordinatensystem in ein anderes

kartesisch - polar:

$$\begin{eqnarray*} r &=& \sqrt{x^2+y^2} \\ \varphi &=& \arctan(y/x) \end{eqnarray*}$$

Was passiert bei $x=0$?

Die Darstellung des Ursprungs ist in polaren Koordinaten nicht eindeutig, wir vereinbaren $\varphi=0$ falls $r=0$.

Bemerkung: Beim Programmieren benutzt man die Funktion double atan2(double y,double x), die den Spezialfall x==0 berücksichtigt und auch alle anderen speziellen Fälle des IEEE-Standards für Gleitkommazahlen (IEEE Std 1003.1, 2004 Edition) korrekt abhandelt (in der Tabelle steht w für den positiven Winkel):

	-inf	-	-0	0	+	+inf	nan	y
-inf	-3pi/2	-pi	-pi	pi	pi	3pi/2	nan
-	-pi/2	-w	-pi	pi	w	pi/2	nan
-0	-pi/2	-pi/2	-pi	pi	pi/2	pi/2	nan
0	-pi/2	-pi/2	-0	0	pi/2	pi/2	nan
+	-pi/2	-w	-0	0	w	pi/2	nan
+inf	-pi/4	-0	-0	0	0	pi/4	nan
nan	nan	nan	nan	nan	nan	nan	nan
x

Bemerkung: Beim Programmieren benutzt man die Funktion double hypot(double x,double y), statt die Wurzel explizit zu berechnen, für die der Standard Folgendes definiert (in der Tabelle steht r für den positiven Radius):

	-inf	-	-0	0	+	+inf	nan	y
-inf	inf	inf	inf	inf	inf	inf	inf
-	inf	r	r	r	r	inf	nan
-0	inf	r	0	0	r	inf	nan
0	inf	r	0	0	r	inf	nan
+	inf	r	r	r	r	inf	nan
+inf	inf	inf	inf	inf	inf	inf	inf
nan	inf	nan	nan	nan	nan	inf	nan
x

polar - kartesisch:

$$\begin{eqnarray*} x &=& r\;\cos\varphi \\ y &=& r\;\sin\varphi \end{eqnarray*}$$

Übung: Umrechnung Kugelkoordinaten in kartesische Koordinaten (mit Berücksichtigung der Spezialfälle).