Zerlegung von Polygonen

Häufig ist es sinnvoll und/oder notwendig, komplexere Polygone in einfachere zu zerlegen. OpenGL stellt z.B. nur konvexe Polygone korrekt dar.

Konvexe Polygone sind einfach zu triangulieren (polarer Scan über die (ja bereits sortierte) Eckenliste):

Dies ergibt Dreiecksfächer (triangle fan) in OpenGL.

Monotone Polygone lassen sich ebenfalls in Linearzeit triangulieren (linearer Scan entlang der monotonen Achse):

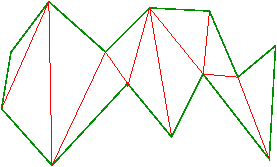
Dies ergibt Dreiecksstreifen (triangle strip und Dreiecksfächer (triangle fan) in OpenGL.

Theoretisch kann man generell einfache Polygone in Linearzeit triangulieren. Das bis jetzt bekannte Verfahren ist aber nicht tauglich für die Praxis. Praktische Lösungen arbeiten mit $O(n \log(n))$ (auch randomisiert mit häufig linearem Verhalten in praktischen Fällen).

Das Zerlegen von einfachen Polygone in konvexe Regionen ist ebenfalls ein unter verschiedenen Gesichtspunkten untersuchtes Problem. Hierbei tritt auf, dass man einerseits schnell Zerteilen möchte, andererseits aber auch möglichst wenige Regionen erhalten möchte.

Verweise auf Computational Geometry (robuste Implementierungen z.B. in CGAL)!